Projection centrale
En géométrie de l'espace, une projection centrale, ou projection conique, ou encore perspective centrale, est définie de la manière suivante. Soit V un point , appelé centre ou sommet de la projection et un plan ne contenant pas V, on appelle projection centrale sur de sommet V, la fonction qui, à tout point A distinct de V, associe le point d'intersection A', s'il existe, de la droite (VA) avec le plan .
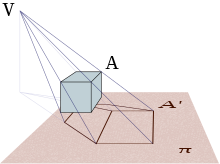

Par exemple, les ombres portées sur une surface plane par une source de lumière ponctuelle est une projection conique
L'étude des projections centrales s'est développée principalement à partir du XVe siècle pour les dessins en perspective linéaire avant d'avoir son développement propre, à partir de 1636, avec les travaux de Girard Desargues, puis ceux de Gaspard Monge et de Jean-Victor Poncelet. Elle a donné naissance à une nouvelle géométrie appelée la géométrie projective.

Présentation et propriétés modifier
Par la suite, on appellera droites et plan centraux, les droites et les plans passant par le centre O d'une projection centrale.
Dans un espace affine modifier
Soit O un point d'un espace affine (en général un plan ou un espace de dimension 3), appelé centre ou sommet de la projection; soit (P) un hyperplan (en général une droite ou un plan) ne contenant pas O ; soit enfin (P') le plan parallèle à (P) passant par O. On appelle projection centrale sur (P) de centre O, l'application de sur (P) qui, à un point M, associe le point d'intersection de la droite (OM) avec l'hyperplan (P)[1].
Remarque : ce point est bien défini puisque M n'appartient pas à (P').
Exemple[2] : Dans , soit (Q) le plan d'équation et (P) celui d'équation et soit la projection de centre O(0,0,0) sur (P). Elle associe, au point de (Q), le point de (P), à condition que soit non nul.
Dans un espace projectif modifier
La projection centrale et ses limites dans les espaces affines a motivé la création des espaces projectifs et a donné naissance à la géométrie projective[3].
La droite projective est née de l'observation d'une projection de centre O sur une droite (d) : tous les points d'une droite passant par O se projettent sur un même point de (d) sauf pour la droite (dO) parallèle à (d) passant par O. Cette exception conduit à imaginer un point dit à l'infini sur lequel tous les points de (dO) vont se projeter. On construit ainsi une bijection entre l'ensemble des droites du plan passant par O et une droite du plan complétée par un point à l'infini. L'idée est donc d'appeler droite projective l'ensemble des droites du plan passant par O, c'est-à-dire l'ensemble des droites vectorielles d'un plan vectoriel. La bijection qui, à toute droite passant par O, associe son intersection avec la droite (d) s'appelle une incidence. Pour tout point M de la droite, on appelle vecteur relevant M, tout vecteur directeur de la droite (OM). Il existe une infinité d'incidences possibles, permettant d'envoyer une des droites quelconque vers l'infini (il suffit de projeter sur une droite parallèle à la droite choisie).
Le plan projectif se construit de la même manière : par projection de centre O sur un plan. L'ensemble des droites passant par O et non parallèles à (P) se projettent sur des points de (P) et on complète (P) par un ensemble de points à l'infini : l'ensemble des droites du plan central passant par (O). Ces points à l'infini forment la droite des infinis[4].
Dans le cas d'une projection centrale sur un plan projectif (P), la droite (OM) rencontre toujours le plan (P), éventuellement à l'infini. La projection centrale est alors définie par tout point différent de O, c'est une application surjective de l'espace privé du point O sur le plan (P).
Le principe se généralise à des espaces projectifs de dimension n. L' ensemble des droites vectorielles d'un espace vectoriel de dimension n+1 est appelé espace projectif de dimension n associé à l'espace vectoriel de dimension n+1. Il peut être vu comme un espace affine de dimension n complété par un ensemble de points dit à l'infini correspondant à l'ensemble des droites vectorielles de l'espace affine.
Cette correspondance permet d'associer à toute projection centrale, une projection vectorielle[5],[6] : Si est l'espace vectoriel associé à E, l'hyperplan de associé à (P) et un vecteur relevant , la projection centrale dans le plan projectif est obtenue par passage au quotient à partir de la projection vectorielle sur selon la direction . C'est donc, quand elle est restreinte à une autre droite projective ne contenant pas une application projective de l'espace projectif. C'est, plus précisément, un cas particulier d'homologie, puisqu'elle possède comme points fixes un hyperplan et un point extérieur à l'hyperplan.
Propriétés modifier
Toutes les propriétés s'entendent pour un espace affine (à condition que les points ou les rapports y soient bien définis) et pour un espace projectif. Les projections conservent l'alignement[7] et les incidences (intersections et contacts[8]) mais ne conservent pas les milieux ni le parallélisme. Elles transforment des faisceaux de droites parallèles en droites parallèles (si la direction des droites est parallèle au plan de projection) ou concourantes. Inversement, deux droites images sont parallèles si et seulement si les droites antécédentes se coupent dans le plan central (P0)[9].
Les projections transforment des droites projectives en droites projectives, des coniques en coniques, des courbes différentiables en courbes différentiables[10].
Les projections centrales conservent le birapport de 4 points. Il existe de nombreuses façons de démontrer cette propriété.
- Une, analytique[11], consiste à se placer dans un repère porté par les droites (OA) et (OB) . Dans ce repère les droites (OC) et (OD) s'expriment sous forme ax + by = 0 et cx + dy =0. On calcule alors les abscisses λc et λd des points C et D dans le repère et on démontre que le birapport est égal à , valeur qui ne dépend que des directions des droites (OA), (OB) (OC) (OD)
- Une, euclidienne, consiste à démontrer que le birapport est égal au birapport des sinus des angles que font les droites entre-elles:
.
- On peut utiliser pour ce faire les aires algébriques des triangles [12] ou les coordonnées polaires des points A, B, C, D dans un repère centré en O et la formule trigonométrique [13].
- Une, affine, consiste à exprimer le birapport comme un rapport simple en utilisant une transversale parallèle à l'une des droites du faisceau: Perrin[14] propose de mener par B une parallèle à (OA) rencontrant (OC) et (OD) en M et N et de démontrer que le birapport est égal . On montre que cette valeur est indépendante de la sécante choisie grâce à une hométhétie de centre O. Cette démarche est peu ou prou celle suivi par Pappus, au IVe siècle, quand il démontre cette propriété dans ses Collections mathématiques. Lehman[15], quant à lui, utilise le point d'intersection M0 de la droite (AB) avec la droite passant par O et parallèle à (A'B'). Il démontre que le birapport (A, B, C, M0) est égal au rapport simple (A', B', C'), à l'aide d'une parallèle à (A'B') passant par C. Par quotient , il démontre que les birapports (A, B, C,D) et (A', B', C', D') sont égaux. Les formules pour les espaces projectifs consiste à prolonger les droites par des points à l'infini[16], le birapport devient alors un rapport simple.
- Une, projective, consiste à remarquer que la projection étant une application projective, elle conserve, comme toute application projective, le birapport. Pour démontrer qu'une application projective conserve le birapport, Audin[17] rappelle qu'une homographie d'une droite sur une droite est déterminée par l'image de 3 points, elle définit le birapport des points ABCD, comme l'image de D par l'homographie de la droite projective (AB) sur la droite projective réelle qui envoie A à l'infini, B en 0 et C en 1. Elle utilise ensuite le fait que la composée d'homographies est une homographie et les caractérise par l'image de 3 points.
Projection d'une droite sur une droite modifier
Dans le plan projectif, si (d1) et (d2) sont deux droites distinctes ne passant pas par O, la restriction à (d1) de la projection centrale de centre O sur (d2) est une bijection dont la réciproque est la projection de centre O de (d2) sur (d1)[18]. C'est un cas particulier d'homographie. Le point infini de (d1) se projette sur le point d'intersection de (d2) avec la parallèle à (d1) passant par O et le point d'intersection de (d1) avec la parallèle à (d2) passant par O se projette sur le point infini de la droite (d2).
Les projections centrales d'une droite sur une autre permettent une démonstration simple du théorème de Pappus[19] et de Desargues[20].
Toute homographie de (d1) sur (d2) peut se décomposer en au plus deux projections. Une homopraphie laissant invariant le point d'intersection des droites est une projection de (d1) sur (d2)[18]. En effet, une homographie de droites est connue par l'image de 3 points. Prenant (I, A, B) sur (d1), et leurs images (I, A', B'), l'homographie coïncide sur ces trois points avec la projection de (d1) sur (d2) de centre O, intersection de (AA') et (BB'). Si I n'est pas invariant, et que l'on connait trois points (A, B, C) et leurs images (A', B', C') un des couples point-image, ne contient ni I, ni I'. En supposant qu'il s'agit de A, on considère le point d'intersection β des droites (AB') et (BA') et le point d'intersection γ des droites (AC') et (CA'). L'homographie coïncide sur les trois points avec la composée de la projection de (d1) sur (βγ) de centre A' suivie de la projection de (βγ) sur (d2) de centre A[21].
Toute homographie de (d) sur (d) ayant un point invariant peut se décomposer en deux projections. Toute homographie quelconque de (d) sur (d) peut se décomposer en au plus trois projections[22].
Généralisation de théorèmes de géométrie classique grâce aux projections coniques modifier
Outre leurs utilités dans le dessin en perspective linéaire, la projection centrale permet d'établir une correspondance entre un plan «classique» celui des cercles et des parallélogrammes avec un plan projectif. Cette correspondance est un outil puissant pour la généralisation des propriétés du cercle et du parallélogramme aux coniques et au quadrilatère complet[23].
Cette correspondance s'exprime sous la forme suivante[24]: Si E est un espace affine et E son complété projectif, si O est un point de E, si (P) et (P') sont deux plans de E ne contenant pas O.
La restriction à P' de la projection centrale de sommet O de E - {O} sur P est une bijection dont la réciproque est la restriction à P de la projection centrale sur P'.
Concernant les points à l'infini, si on appelle (PO) et (P'O) les plans parallèles à (P) et (P') passant par O, les droites à l'infini de P et P', notées (di,P) et (di,P') sont caractérisées par[24]
Le cas du quadrilatère complet modifier
Un quadrilatère complet est la donnée de 4 droites dont trois ne sont jamais concourantes, ces 4 droites produisent 6 points d'intersections qui sont les sommets du quadrilatère. Ces 6 points produisent trois autres droites distinctes des 4 droites précédentes appelés diagonales du quadrilatère complet. Ces trois diagonales génèrent 3 points, appelés points d'intersection des diagonales.
Tout quadrilatère complet peut être vu comme image par projection centrale d'un parallélogramme[25].
Cette correspondance permet d'exhiber les faisceaux harmoniques d'un quadrilatère complet à partir des faisceaux harmoniques dans un parallélogramme Pour un parallélogramme, le faisceau formé par les diagonales et les médianes est un faisceau harmonique. Il suffit pour s'en convaincre de remarquer que le birapport [A,B, I, ∞] vaut -1. On en déduit que dans le parallélogramme complet ci-contre, (IK),(IJ),(IE), (IF) est également un faisceau harmonique et que les points (EFKJ) forment une division harmonique.
De même, dans un parallélogramme, le faisceau de droites parallèles formé des supports de deux côtés opposés, de la médiane et de la droite à l'infini est un faisceau harmonique, il en est de même du faisceau (EA), (EC), (EI), (EF) et les points (ACIK) forment une division harmonique.
Le cas des triangles homologiques modifier
Deux triangles (ABC) et (A'B'C') sont dits homologiques si les points d'intersection de (AB) avec (A'B'), de (BC) avec (B'C'), et de (CA) avec (C'A') sont alignés sur une droite d.
Toute paire de triangles homologiques peut être vue comme image par projection centrale d'une paire de triangles homothétiques ou translatés l'un de l'autre[25]. Il suffit de prendre un plan parallèle au plan contenant (d) et passant par O. Par projection centrale dans ce plan les droites images de (AB) et (A'C') (respectivement de (BC) et (B'C'), de (CA) et (C'A') sont parallèles. Cette correspondance permet de mettre en rapport la version projective et la version affine du théorème de Desargues[26].
Le cas des coniques modifier
Les projections centrales trouvent une grande part de leur intérêt dans l'étude des coniques. En effet, l'image d'un cercle par une projection centrale est une conique et, inversement, une conique étant définie comme l'intersection d'un cône de révolution par un plan, elle peut être vue comme l'image d'un cercle par une projection centrale dont le centre est sur l'axe du cercle[27]. Toutes les propriétés touchant le cercle et concernant les invariants des projections centrales (alignement, contact, birapport) peuvent être transférées à toute conique. Il en est ainsi du birapport de 4 points sur une conique, défini comme le birapport des quatre droites issues d'un point quelconque de la conique et passant chacune par un des 4 points en question. Cette notion se déduit de celle de birapport sur un cercle[28]. Il en est de même du théorème de Pascal concernant l'hexagone inscrit dans une conique qui se déduit de celui de l'hexagone inscrit dans un cercle.
Notes et références modifier
- François Le Lionnais, Michel George et Alain Bouvier, Dictionnaire des mathématiques, Presses universitaires de France, (ISBN 2-13-052025-1 et 978-2-13-052025-2, OCLC 469353783), p. 133
- Daniel Perrin, « Géométrie projective linéaire, p.5 »
- Perrin 20??, p. 5;6.
- Audin 2006, p. 183.
- Tauvel 2005, p. 182.
- Perrin 20??, p. 30 1.7.5..
- Lehman et Bkouche 1988, p. 101.
- Lehman et Bkouche 1988, p. 102.
- Lehman et Bkouche 1988, p. 117.
- Lehman et Bkouche 1988, p. 103.
- Tauvel 2005, p. 134.
- pour par exemple ce TIPE p. 10
- Voir par exemple ces notes de cours
- Perrin 20??, p. 71 3.8.1..
- Lehman et Bkouche 1988, p. 107.
- Lehman et Bkouche 1988, p. 114.
- Audin 2006, p. 197.
- Perrin 20??, p. 34.
- Perrin 20??, p. 35.
- Perrin 20??, p. 38.
- Perrin 20??, p. 42 2.5.3..
- Perrin 20??, p. 43 2. 5. 4..
- Lehman et Bkouche 1988, p. 122.
- Lehman et Bkouche 1988, p. 120.
- Lehman et Bkouche 1988, p. 126.
- Lehman et Bkouche 1988, p. 128.
- Lehman et Bkouche 1988, p. 130.
- Lehman et Bkouche 1988, p. 135.
Bibliographie modifier
- Daniel Lehman et Rudolphe Bkouche, Initiation à la géométrie, Paris, PUF, ;
- Patrice Tauvel, Géométrie : Agrégation, licence 3e année, Master, Paris, Dunod, ;
- Marcel Berger, Géométrie : Action de groupes, espaces affines et projectifs, vol. 1, CEDIC/Nathan, ;
- Michèle Audin, Géométrie : L3M1, EDP sciences, .
- Daniel Perrin, Projet de livre de géométrie projective, Université Paris-Saclay, 20?? (lire en ligne).
