Théorème de factorisation
En mathématiques, le théorème de factorisation est un principe général qui permet de construire un morphisme d'une structure quotient dans un autre espace à partir d'un morphisme de vers , de façon à factoriser ce dernier par la surjection canonique de passage au quotient.
Le cas des ensembles modifier
Soit un ensemble muni d'une relation d'équivalence et la surjection canonique.
Théorème — Soit une application telle que (pour toute paire d'éléments x, x' dans X)
Alors, il existe une unique application
De plus :
- est injective si et seulement si, réciproquement, (et donc si ) ;
- est surjective si et seulement si est surjective ;
- est bijective si est surjective et si .
(La réciproque est moins utile mais immédiate : pour toute application g : X/R → Y, la composée f = g∘s vérifie x R x' ⇒ f(x) = f(x').)
Ce théorème peut se spécialiser à un certain nombre de structures algébriques ou topologiques.
Le cas des groupes modifier
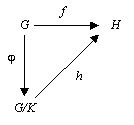
Sur un groupe , on considère la relation d'équivalence définie par un sous-groupe normal de : si . Alors, la surjection canonique est un morphisme de groupes et le théorème de factorisation s'énonce
Théorème — Soit un morphisme de groupes. Si est contenu dans le noyau de , alors il existe un unique morphisme de groupes tel que . De plus :
- est surjectif si est surjectif ;
- est injectif si on a ;
- est un isomorphisme si est surjectif et .
Le cas des espaces vectoriels modifier
On considère un espace vectoriel et la relation d'équivalence définie par un sous-espace vectoriel : si . Alors, la surjection canonique est linéaire.
Théorème — Soit une application linéaire. Si est contenu dans le noyau de , alors il existe une unique application linéaire telle que . De plus :
- est surjective si est surjective ;
- est injective si on a ;
- est un isomorphisme si est surjective et .
Le cas des anneaux modifier
On considère un anneau et la relation d'équivalence définie par un idéal bilatère de : si . Alors, la surjection canonique est un morphisme d'anneaux.
Théorème — Soit un morphisme d'anneaux. Si est contenu dans le noyau de , alors il existe un unique morphisme d'anneaux tel que . De plus :
- est surjectif si est surjectif ;
- est injectif si on a ;
- est un isomorphisme si est surjectif et .
Le cas des espaces topologiques modifier
Soit un espace topologique muni d'une relation d'équivalence et la surjection canonique. On munit de la topologie quotient. Soit une application continue.
Théorème — Si pour tout couple dans , on a , alors il existe une unique application continue telle que . De plus :
- est surjective si est surjective ;
- est injective si on a équivalent à ;
- est ouverte (resp. fermée) si est ouverte (resp. fermée) ;
- est un homéomorphisme si est surjective et ouverte ou fermée, et si .
Références modifier
- N. Bourbaki, Éléments de mathématique : Théorie des ensembles [détail des éditions], p. II-44, C57, renvoyant à p. II-20 sur Google Livres, proposition 9.a.
- Saunders Mac Lane et Garrett Birkhoff, Algèbre [détail des éditions], p. 35 de l'éd. de 1999 en anglais sur Google Livres.


