Loi bêta prime
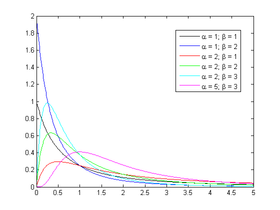
Densité de probabilité
Fonction de répartition
Paramètres
α
>
0
{\displaystyle \alpha >0}
paramètre de forme
β
>
0
{\displaystyle \beta >0}
Support
x
∈
]
0
,
∞
[
{\displaystyle x\in ]0,\infty [}
Densité de probabilité
f
(
x
)
=
x
α
−
1
(
1
+
x
)
−
α
−
β
B
(
α
,
β
)
{\displaystyle f(x)={\frac {x^{\alpha -1}(1+x)^{-\alpha -\beta }}{B(\alpha ,\beta )}}\!}
Fonction de répartition
I
x
1
+
x
(
α
,
β
)
{\displaystyle I_{{\frac {x}{1+x}}(\alpha ,\beta )}}
I
x
(
α
,
β
)
{\displaystyle I_{x}(\alpha ,\beta )}
Espérance
α
β
−
1
si
β
>
1
{\displaystyle {\frac {\alpha }{\beta -1}}{\text{ si }}\beta >1}
Mode
α
−
1
β
+
1
si
α
≥
1
, 0 sinon
{\displaystyle {\frac {\alpha -1}{\beta +1}}{\text{ si }}\alpha \geq 1{\text{, 0 sinon}}\!}
Variance
α
(
α
+
β
−
1
)
(
β
−
2
)
(
β
−
1
)
2
si
β
>
2
{\displaystyle {\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2}}}{\text{ si }}\beta >2}
modifier
En théorie des probabilités et en statistique , la loi bêta prime (également connue sous les noms loi bêta II ou loi bêta du second type [ 1] loi de probabilité continue définie dont le support est
]
0
,
+
∞
[
{\textstyle ]0,+\infty [}
paramètres de forme .
Si une variable aléatoire X suit une loi bêta prime, on notera
X
∼
β
′
(
α
,
β
)
{\displaystyle X\sim \beta ^{'}(\alpha ,\beta )}
Sa densité de probabilité est donnée par :
f
(
x
)
=
{
x
α
−
1
(
1
+
x
)
−
α
−
β
B
(
α
,
β
)
si
x
>
0
0
sinon.
{\displaystyle f(x)={\begin{cases}{\frac {x^{\alpha -1}(1+x)^{-\alpha -\beta }}{\mathrm {B} (\alpha ,\beta )}}&{\text{ si }}x>0\\0&{\text{ sinon.}}\end{cases}}}
où B est la fonction bêta .
Cette loi est une loi de Pearson de type VI[ 1]
Le mode d'une variable aléatoire de loi bêta prime est
X
^
=
α
−
1
β
+
1
{\displaystyle {\widehat {X}}={\frac {\alpha -1}{\beta +1}}}
α
β
−
1
{\displaystyle {\frac {\alpha }{\beta -1}}}
β
>
1
{\displaystyle \beta >1}
β
≤
1
{\displaystyle \beta \leq 1}
variance est
α
(
α
+
β
−
1
)
(
β
−
2
)
(
β
−
1
)
2
{\displaystyle {\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2}}}}
β
>
2
{\displaystyle \beta >2}
Pour
−
α
<
k
<
β
{\displaystyle -\alpha <k<\beta }
k -ième moment
E
[
X
k
]
{\displaystyle \mathbb {E} [X^{k}]}
E
[
X
k
]
=
B
(
α
+
k
,
β
−
k
)
B
(
α
,
β
)
.
{\displaystyle \mathbb {E} [X^{k}]={\frac {\mathrm {B} (\alpha +k,\beta -k)}{\mathrm {B} (\alpha ,\beta )}}.}
Pour
k
∈
N
{\displaystyle k\in \mathbb {N} }
k
<
β
{\displaystyle k<\beta }
E
[
X
k
]
=
∏
i
=
1
k
α
+
i
−
1
β
−
i
.
{\displaystyle \mathbb {E} [X^{k}]=\prod _{i=1}^{k}{\frac {\alpha +i-1}{\beta -i}}.}
La fonction de répartition de la loi bêta prime est :
F
(
x
)
=
{
x
α
⋅
2
F
1
(
α
,
α
+
β
,
α
+
1
,
−
x
)
α
⋅
B
(
α
,
β
)
si
x
>
0
0
sinon.
{\displaystyle F(x)={\begin{cases}{\frac {x^{\alpha }\cdot _{2}F_{1}(\alpha ,\alpha +\beta ,\alpha +1,-x)}{\alpha \cdot \mathrm {B} (\alpha ,\beta )}}&{\text{ si }}x>0\\0&{\text{ sinon.}}\end{cases}}}
où
2
F
1
{\displaystyle _{2}F_{1}}
fonction hypergéométrique .
De nouveaux paramètres peuvent être ajoutés pour former la loi bêta prime généralisée :
p
>
0
{\displaystyle p>0}
paramètre de forme et
q
>
0
{\displaystyle q>0}
paramètre d'échelle .La densité de probabilité est alors donnée par :
f
(
x
;
α
,
β
,
p
,
q
)
=
{
p
(
x
q
)
α
p
−
1
(
1
+
(
x
q
)
p
)
−
α
−
β
q
B
(
α
,
β
)
si
x
>
0
0
sinon.
{\displaystyle f(x;\alpha ,\beta ,p,q)={\begin{cases}{\frac {p{\left({\frac {x}{q}}\right)}^{\alpha p-1}\left({1+{\left({\frac {x}{q}}\right)}^{p}}\right)^{-\alpha -\beta }}{q\mathrm {B} (\alpha ,\beta )}}&{\text{ si }}x>0\\0&{\text{ sinon.}}\end{cases}}}
avec moyenne
q
Γ
(
α
+
1
p
)
Γ
(
β
−
1
p
)
Γ
(
α
)
Γ
(
β
)
si
β
p
>
1
{\displaystyle {\frac {q\Gamma (\alpha +{\tfrac {1}{p}})\Gamma (\beta -{\tfrac {1}{p}})}{\Gamma (\alpha )\Gamma (\beta )}}{\text{ si }}\beta p>1}
et mode
q
(
α
p
−
1
β
p
+
1
)
1
p
si
α
p
≥
1.
{\displaystyle q{\left({\frac {\alpha p-1}{\beta p+1}}\right)}^{\tfrac {1}{p}}{\text{ si }}\alpha p\geq 1.}
Si une variable aléatoire X suit une loi bêta prime généralisée, on notera
X
∼
β
′
(
α
,
β
,
p
,
q
)
{\displaystyle X\sim \beta ^{'}(\alpha ,\beta ,p,q)}
p =q =1, alors la loi bêta prime généralisée est la loi bêta prime standard.
Loi gamma composée
modifier
La loi gamma composée [ 2] p =1 et q est quelconque. Elle est nommée ainsi car elle est une composition de deux lois gamma dans le sens :
β
′
(
x
;
α
,
β
,
1
,
q
)
=
∫
0
∞
G
(
x
;
α
,
p
)
G
(
p
;
β
,
q
)
d
p
{\displaystyle \beta '(x;\alpha ,\beta ,1,q)=\int _{0}^{\infty }G(x;\alpha ,p)G(p;\beta ,q)\;\mathrm {d} p}
où G (x ; a , b ) est la loi gamma avec forme a et intensité b . Cette relation peut être utilisée pour générer des variables aléatoires de loi gamma composée ou de loi bêta prime.
Les mode, moyenne et variance de la loi gamma composée peuvent être obtenus en multipliant les mode et moyenne de la loi bêta prime par q et la variance par q 2 .
Si
X
∼
β
′
(
α
,
β
)
{\displaystyle X\sim \beta ^{'}(\alpha ,\beta )\,}
1
X
∼
β
′
(
β
,
α
)
{\displaystyle {\tfrac {1}{X}}\sim \beta ^{'}(\beta ,\alpha )}
Si
X
∼
β
′
(
α
,
β
,
p
,
q
)
{\displaystyle X\sim \beta ^{'}(\alpha ,\beta ,p,q)\,}
k
X
∼
β
′
(
α
,
β
,
p
,
k
q
)
{\displaystyle kX\sim \beta ^{'}(\alpha ,\beta ,p,kq)\,}
β
′
(
α
,
β
,
1
,
1
)
=
β
′
(
α
,
β
)
{\displaystyle \beta ^{'}(\alpha ,\beta ,1,1)=\beta ^{'}(\alpha ,\beta )\,}
Liens avec d'autres lois
modifier
Si
X
∼
F
(
α
,
β
)
{\displaystyle X\sim F(\alpha ,\beta )\,}
α
β
X
∼
β
′
(
α
2
,
β
2
)
{\displaystyle {\tfrac {\alpha }{\beta }}X\sim \beta ^{'}({\tfrac {\alpha }{2}},{\tfrac {\beta }{2}})\,}
F est la loi de Fisher )
Si
X
∼
Beta
(
α
,
β
)
{\displaystyle X\sim {\textrm {Beta}}(\alpha ,\beta )\,}
X
1
−
X
∼
β
′
(
α
,
β
)
{\displaystyle {\frac {X}{1-X}}\sim \beta ^{'}(\alpha ,\beta )\,}
Si
X
∼
Γ
(
α
,
1
)
{\displaystyle X\sim \Gamma (\alpha ,1)\,}
Y
∼
Γ
(
β
,
1
)
{\displaystyle Y\sim \Gamma (\beta ,1)\,}
X
Y
∼
β
′
(
α
,
β
)
{\displaystyle {\frac {X}{Y}}\sim \beta ^{'}(\alpha ,\beta )}
β
′
(
p
,
1
,
a
,
b
)
=
Dagum
(
p
,
a
,
b
)
{\displaystyle \beta ^{'}(p,1,a,b)={\textrm {Dagum}}(p,a,b)\,}
loi de Dagum
β
′
(
1
,
p
,
a
,
b
)
=
SinghMaddala
(
p
,
a
,
b
)
{\displaystyle \beta ^{'}(1,p,a,b)={\textrm {SinghMaddala}}(p,a,b)\,}
loi de Burr
β
′
(
1
,
1
,
γ
,
σ
)
=
LL
(
γ
,
σ
)
{\displaystyle \beta ^{'}(1,1,\gamma ,\sigma )={\textrm {LL}}(\gamma ,\sigma )\,}
loi log-logistique
↑ a et b Johnson et al (1995), p248
↑ (en) Satya D. Dubey , « Compound gamma, beta and F distributions », Metrika vol. 16, décembre 1970 , p. 27–31 (DOI 10.1007/BF02613934 lire en ligne ) (en) Jonhnson, N.L., Kotz, S. et Balakrishnan, N., Continuous Univariate Distributions , vol. 2, Wiley, 1995 (ISBN 0-471-58494-0 (en) Eric W. Weisstein , « Beta Prime Distribution MathWorld
![{\displaystyle x\in ]0,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bb4644f4578b19659b5ca8c206451b09775b622)
![{\textstyle ]0,+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68a04bef51657e5d237ddab5946a79f1b3f0e7d1)
![{\displaystyle \mathbb {E} [X^{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26834d622db9fd3386774a4ae55e19796ed59daa)
![{\displaystyle \mathbb {E} [X^{k}]={\frac {\mathrm {B} (\alpha +k,\beta -k)}{\mathrm {B} (\alpha ,\beta )}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/853c7253e8c33a2ae1dc1f9123db0a8db6315041)
![{\displaystyle \mathbb {E} [X^{k}]=\prod _{i=1}^{k}{\frac {\alpha +i-1}{\beta -i}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20c22a219aabbfed99e6ee166e76871a818538da)
