Inégalité arithmético-géométrique
En mathématiques, l'inégalité arithmético-géométrique (IAG) établit un lien entre la moyenne arithmétique et la moyenne géométrique. C'est un résultat classique lié à la convexité.
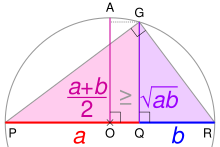
Énoncé modifier
La moyenne géométrique de réels strictement positifs est inférieure à leur moyenne arithmétique :
avec égalité (si et) seulement si .
Démonstrations modifier
Les deux réels (moyenne arithmétique) et (moyenne géométrique) étant strictement positifs, l'inégalité à démontrer équivaut (par croissance stricte du logarithme naturel) à
ou encore (d'après l'équation fonctionnelle du logarithme) à
Cette dernière inégalité n'est autre que l'inégalité de Jensen pour des isobarycentres, appliquée à la fonction logarithme, qui est concave.
Le cas d'égalité provient du fait que cette concavité est stricte.
L'inégalité arithmético-géométrique peut également être démontrée comme un corollaire de l'inégalité de Muirhead, appliquée aux suites (1,0, … , 0) et (1/n, … , 1/n).
On peut également utiliser les multiplicateurs de Lagrange en étudiant les maximums de la fonction sur l'ensemble .
Preuve de Pólya modifier
George Pólya prouve l'inégalité arithmético-géométrique en considérant[1] :
On considère ensuite a1, a2, ..., an des nombres réels positifs. On pose ensuite :
On utilise l'inégalité ci-dessus pour les nombres ak/A, ce qui donne :
dont le produit donne :
soit
ce qui permet de conclure. On remarque alors qu'on atteint l'égalité s'il y a égalité dans chacune des inégalités précédentes, donc si les ai sont tous égaux (à A)[2].
Preuve d'Aizer modifier
Horst Aizer donne cette preuve[3] : soit f une fonction réelle continue telle qu'il existe x0 vérifiant
On a alors :
On applique ce résultat à f(t) = –1/t :
On en déduit
soit
donc ln(G/x0) ≤ A⁄x0 – 1. Considérer x0 = A ou G permet de conclure.
Preuve de Schlömilch modifier
Oskar Schlömilch donne une preuve élémentaire[4]. On considère l'identité :
qu'on peut obtenir en dérivant l'expression 1 – zn+11 – z de deux façons différentes. Le membre de gauche est positif pour z positif. On a donc, pour z positif :
avec égalité en z = 1. La substitution donne
avec égalité si et seulement si x = y. On retrouve alors une inégalité arithmético-géométrique pondérée. On finit par récurrence sur n pour conclure.
Preuve matricielle modifier
Fergus Gaines donne une preuve[5] reposant sur une inégalité de Schur[6] : soit M une matrice carrée de valeurs propres λ1, λ2, ... , λn, alors on a, par le résultat de Schur,
avec égalité si et seulement si M est normale. Appliquée à la matrice
en remarquant que Mn = √a1…an In, on a Le résultat de Schur donne directement l'inégalité arithmético-géométrique, avec égalité si et seulement si diag(a1, a2, … , an) = diag(an, a1, … , an–1), c.-à-d. si les ai sont tous égaux.
Généralisations modifier
Pondération modifier
L'inégalité arithmético-géométrique se généralise aux moyennes pondérées arithmétique et géométrique :
Si et alors, en notant :
avec égalité si et seulement si tous les sont égaux.
En effet, en supposant sans perte de généralité qu'aucun n'est nul et en notant (strictement positifs et de somme ), l'inégalité équivaut (voir supra) à
- ,
qui n'est autre que l'inégalité de Jensen générale pour la fonction (concave) logarithme, et le cas d'égalité provient de la stricte concavité.
Inégalité de Maclaurin modifier
On peut également généraliser l'inégalité arithmético-géométrique en remarquant que la moyenne arithmétique correspond à la première fonction symétrique élémentaire, et la moyenne géométrique à la dernière. L'inégalité arithmético-géométrique se réécrit :
Et on peut généraliser :
soit
Ce sont les inégalités de Maclaurin.
Majoration de l'écart modifier
Il existe une majoration de l'écart entre les deux moyennes : [7],
qui est une égalité pour : .
Cette inégalité est une conséquence de l'inégalité de convexité de Vasile Cîrtoaje : [8] , pour une fonction convexe, en prenant et .
Références modifier
- Hardy, Littlewood et Pólya 1952.
- (en) Ross Honsberger, Mathematical Morsels, (lire en ligne), Problem 26.
- (en) Horst Aizer, « A proof of the arithmetic mean-geometric mean inequality », Amer. Math. Monthly, vol. 103, no 7, , p. 585.
- (de) O. Schlömilch, « Über Mïttelgrössen verschiedener Ordnungen », Zeitschrift für Mathematik und Physik, vol. 3, , p. 308-10.
- (en) Fergus Gaines, « On the arithmetic mean-geometric mean inequality », Amer. Math. Monthly, vol. 74, , p. 305-306 (lire en ligne).
- (de) I. Schur, « Über die charakteristischen Wurzeln einer linearen Substitution mit einer Anwendung auf die Theorie der Integralgleichungen », Math. Ann., vol. 66, , p. 488-510 (lire en ligne).
- Rémy Eupherte, « Une majoration de l'écart entre moyenne algébrique et géométrique », Bulletin de l'UPS, (lire en ligne)
- (en) Darij Grinberg, « Generalizations of Popoviciu’s inequality »
Voir aussi modifier
Articles connexes modifier
Lien externe modifier
- René Adad, Moyennes arithmétique et géométrique.
Bibliographie modifier
- Augustin Cauchy, Œuvres complètes, Gauthier-Villard, (lire en ligne), « Cours d'analyse », p. 376, lire en ligne sur Gallica
- Martin Aigner et Günter M. Ziegler, Raisonnements divins, Springer, , 2e éd. (lire en ligne), p. 127-129
- (en) Peter S. Bullen, Handbook of Means and Their Inequalities, Kluwer Academic Publishers, (lire en ligne), p. 71-153
- (en) G. H. Hardy, J. E. Littlewood et G. Pólya, Inequalities, CUP, , 2e éd. (lire en ligne), p. 16-21