Nombre pentagonal
En mathématiques, un nombre pentagonal est un nombre figuré qui compte des points régulièrement répartis dans un pentagone.
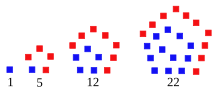

Pour tout entier ≥ 1, d'après les formules générales pour les nombres polygonaux, à l'étape où il y a points dans chaque côté du pentagone, le nombre pentagonal est la somme des premiers termes de la suite arithmétique de premier terme 1 et de raison 3[1] :
soit le tiers du (3 – 1)-ième nombre triangulaire.
Les dix premiers sont 1, 5, 12, 22, 35, 51, 70, 92, 117 et 145 (suite A000326 de l'OEIS).
Les nombres pentagonaux sont importants dans la théorie des partitions d'entiers d'Euler et interviennent par exemple dans son théorème des nombres pentagonaux.
Obtention de ces nombres modifier
Pour avoir points sur chaque côté du pentagone extérieur, on ajoute à l'étape : points aux sommets du pentagone et points à l'intérieur des côtés, d'où .
Donc
Autre construction modifier
De la formule générale , découle que est la somme du nombre carré d'ordre : et du nombre triangulaire d'ordre : .
Propriétés modifier
- est congru à modulo 3.
- .
- D'après le théorème des nombres polygonaux de Fermat, tout entier naturel est la somme d'au plus 5 nombres pentagonaux.
Test des nombres pentagonaux modifier
Un réel positif x est un nombre pentagonal si et seulement si l'équation du second degré 3n2 – n – 2x possède une solution entière > 0, c'est-à-dire si le réel suivant est entier :
Lorsque est entier, x est le -ième nombre pentagonal.
Nombres pentagonaux généralisés modifier
Les nombres pentagonaux généralisés sont les nombres de la forme n(3n – 1)/2, mais avec n entier relatif, ou encore : les nombres de la forme n(3n ± 1)/2 avec n entier naturel. Les vingt premiers termes de cette suite d'entiers sont 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126 et 145 (suite A001318 de l'OEIS).
Notes et références modifier
- Jean Itard, Arithmétique et théorie des nombres, Paris, PUF, , 128 p. (ISBN 978-2130324300), p. 8.
- Roger B. Nelsen, Preuves sans mots, Hermann, , p. 214
- ACL, Preuves en images, t. 1, Les Éditions du Kangourou, (présentation en ligne), p. 14
Voir aussi modifier
Articles connexes modifier
Liens externes modifier
- « Nombre pentagonal », sur recreomath.qc.ca
- Gérard Villemin, « Nombre pentagonal »

