Grand axe
En géométrie, un grand axe d'une ellipse, d'un ellipsoïde ou d'un hyperellipsoïde est un diamètre de longueur maximale de cette courbe, surface ou hypersurface. C’est l’unique segment reliant les points d’intersections avec elle de son axe de symétrie principal lorsqu’elle n’est pas un cercle, une sphère ou une hypersphère, ou de n’importe lequel de ses axes de symétrie si c’en est un ou une.
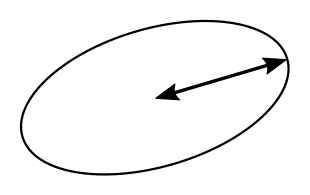
Un demi-grand axe (en latin : semiaxis maior) en est une moitié d’un grand axe, dont l’une des extrémités est ainsi le centre de l’(hyper)ellips(oïd)e. Si l'objet est un cercle, une sphère ou une hypersphère, un demi-grand axe (ou un demi-petit axe) en est un rayon.
Formulation analytique
modifierL'équation cartésienne normalisée d'une quadrique en dimension quelconque (son équation dans un repère orthonormé ayant pour origine le centre de la quadrique et pour directions celles de ses axes principaux) est :
où D est la dimension de l'espace, les les D coordonnées et les D constantes (choisies positives).
Le demi-grand axe est la plus grande de ces constantes, .
Cas particulier des ellipses et des ellipsoïdes ou hyperellipsoïdes de révolution oblongs
modifierDéfinition alternative
modifierUne ellipse (ou, à plus de deux dimensions, un ellipsoïde ou hyperellipsoïde de révolution oblong) est l'ensemble des points M de l'espace (le plan dans le cas d'une ellipse) dont la somme des distances à deux points fixes F et F' est constante. Cette constante, notée , est le grand axe de :
- .
Propriétés géométriques
modifierLe grand axe d'une ellipse est son plus grand diamètre, un segment qui traverse à la fois le centre et les deux foyers de l'ellipse et la rejoint en ses deux points les plus opposés. Le demi-grand axe correspond à la moitié du grand axe et joint le centre et un bord de l'ellipse à travers l'un des foyers.
De façon similaire, le segment perpendiculaire au grand axe, passant par le centre et rejoignant l'ellipse est son petit axe. Les axes sont les équivalents elliptiques des diamètres d'un cercle, tandis que les demi-axes sont les analogues des rayons.
Notions connexes
modifierExcentricité
modifierLa longueur du demi-grand axe et celle du demi-petit axe sont liées par l'excentricité et le « paramètre » de l’ellipse, généralement noté p, représentant le demi latus rectum (corde parallèle à la directrice et passant par le foyer) :
Cercle principal
modifierLe cercle de centre , le centre d'une ellipse , et de diamètre , le grand axe de l'ellipse, est le cercle principal de l'ellipse.
L'ellipse est l'image du cercle principal par l'affinité orthogonale de base Ox et de rapport .
Notions équivalentes
modifierLe cercle étant une ellipse d'excentricité linéaire nulle, le grand axe d'un cercle est son diamètre et son demi-grand axe son rayon.
L'hyperbole est une conique d'excentricité linaire supérieure à 1. L'axe transverse d'une hyperbole, segment de la droite qui traverse le centre et les deux foyers de l'hyperbole, est l'équivalent du demi-grand axe d'une ellipse. L'axe conjugué d'une hyperbole, segment de la droite compris entre l'un des sommets de l'hyperbole et l'une des droites asymptotes à la courbe de même sommet, est l'équivalent au demi-petit axe d'une ellipse.
Astronomie
modifierPériode orbitale
modifierEn astronomie, le demi-grand axe est un élément orbital important, permettant de définir partiellement une orbite. De façon générale, dans le cadre d'un problème à deux corps, le carré de la période orbitale d'un corps de masse orbitant autour d'un autre corps de masse est :
où :
- est la longueur du demi-grand axe ;
- est la constante gravitationnelle.
Si l'un des corps est suffisamment petit pour que sa masse soit négligée par rapport à l'autre :
où est le paramètre gravitationnel standard.
Dans ce cas, pour toutes les orbites de même demi-grand axe, la période est la même quelle que soit l'excentricité.
On obtient donc la proportionnalité suivante :
ce qui correspond à la troisième loi de Kepler.
Distance moyenne
modifierLe demi-grand axe ne correspond pas forcément à la distance moyenne entre les deux corps en orbite, car cette distance dépend du procédé utilisé :
- En calculant la moyenne de la distance sur l'anomalie excentrique, on trouve effectivement le demi-grand axe.
- La moyenne sur l'anomalie vraie donne le demi-petit axe.
- Moyenner sur l'anomalie moyenne conduit à la valeur .
Par ailleurs, le « rayon moyen de l'ellipse », qui désigne en fait le rayon du cercle de même aire, est .
Voir aussi
modifierArticles connexes
modifierLiens externes
modifier- (en) « Semi-major / Semi-minor axis of an ellipse », sur mathopenref.com (avec animation interactive)