Loi de Titius-Bode

La loi de Titius-Bode ou Rang des planètes, souvent appelée loi de Bode, est une relation empirique entre les rayons des orbites des planètes du Système solaire, qui utilise une suite arithmético-géométrique de raison 2.

Elle a été énoncée en 1766 par Johann Daniel Titius, qui avait trouvé une relation numérique dans les termes de la suite des distances des planètes, citées en 1724 par le philosophe Christian Wolff. Celui-ci n'avait fait d’ailleurs que recopier la suite des nombres 4, 7, 10, 15, 52, 95, mentionnée en 1702 par le mathématicien écossais David Gregory, qui représentait les distances des planètes en 1/10 du rayon de l’orbite terrestre. Mais c’est à Johann Elert Bode qu’est longtemps revenue la paternité de cette « loi », qu'il avait publiée en 1772 dans Anleitung zur Kenntniß des gestirnten Himmels (« Instruction pour la connaissance du ciel étoilé »).

Corroborée en 1781 par la découverte d'Uranus, la loi de Bode est mise en échec en 1846 par celle de Neptune et ne donne plus de résultats probants au-delà.

Distances relatives entre les planètes du Système solaire (les tailles des planètes ne sont pas à l'échelle).

Expression mathématique

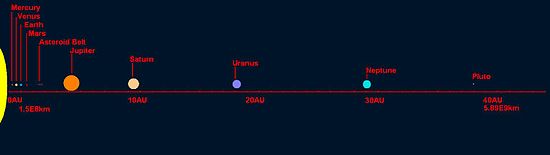
L'expression d'origine exprimait les distances en dixièmes de la distance Terre-Soleil (en unité astronomique, symbole « au »). Les distances supposées sont :

• pour Mercure : 4 + (3 × 0) = 4
• pour Vénus : 4 + (3 × 1) = 7
• pour la Terre : 4 + (3 × 2) = 10
• pour Mars : 4 + (3 × 4) = 16
• etc.

En termes mathématiques, la formule exprimant la distance de la planète au Soleil est une suite arithmético-géométrique :

$r=0{,}4+0{,}3\times 2^{n-1}$

où r est exprimé en unités astronomiques ;

n est le « rang » de la planète : -∞ (moins l'infini) pour Mercure, 1 pour Vénus, 2 pour la Terre, 3 pour Mars, 4 pour la ceinture d'astéroïdes, 5 pour Jupiter, 6 pour Saturne, etc.

Une variante d'écriture est par exemple : $r=0{,}4+0{,}15\times 2^{n}$.

Faiblesses intrinsèques

La première faiblesse de cette loi est l'utilisation de -∞ comme rang pour Mercure, qui brise le caractère arithmético-géométrique de la suite. La seule raison de ce -∞ est de faire mieux correspondre la loi à la réalité.

La seconde faiblesse est que, quand la loi fut formulée, le rang 4 semblait inoccupé ; la découverte de la ceinture d'astéroïdes sembla conforter la loi, mais on peut critiquer le fait d'intégrer à cette loi la ceinture alors que tous les astéroïdes réunis n'ont pas la masse d'une planète. Si l'on cherche à donner une explication, il faut alors aussi expliquer pourquoi cette ceinture prend la place d'une planète.

Enfin, il n'a jamais été précisé ce que signifie « rayon » ou « distance » dans l'énoncé de la loi. En effet, pour que ces notions soient clairement définies, il faudrait que les orbites soient parfaitement circulaires. C'est loin d'être le cas des planètes à proprement parler (Mercure en particulier, dont la distance au Soleil varie d'un facteur 1,5) et certains objets qu'on tenta d'ajouter à la progression l'étaient encore moins. Généralement, on retient le demi-grand axe comme distance.

Planète	Loi de Titius-Bode		Valeurs réelles				Erreur
	Rang attribué	Distance prédite	Demi-grand axe	Périphélie	Aphélie	Excentricité	absolue	relative
Mercure	-∞	0,4	0,387	0,307	0,467	0,206	0,013	3,4 %
Vénus	1	0,7	0,723	0,718	0,728	0,007	0,023	3,2 %
Terre	2	1,0	1,000	0,983	1,017	0,017	0,000	0,0 %
Mars	3	1,6	1,523	1,381	1,665	0,093	0,077	5,1 %
Cérès	4	2,8	2,765	2,547	2,983	0,079	0,035	1,3 %
Jupiter	5	5,2	5,203	4,953	5,453	0,048	0,003	0,1 %
Saturne	6	10,0	9,537	9,022	10,052	0,054	0,463	4,9 %
Uranus	7	19,6	19,229	18,325	20,133	0,047	0,371	1,9 %
Neptune	8	38,8	30,069	29,798	30,340	0,009	8,731	29,0 %

Découvertes ultérieures

Lors de sa publication originelle, la loi était vérifiée par toutes les planètes connues, de Mercure à Saturne, avec une lacune entre les quatrième (n = 3) et cinquième (n = 5) planètes. Cette loi était alors considérée comme intéressante mais sans grande importance. La découverte d'Uranus, dont l'orbite respecte la loi, la valida aux yeux d'une grande partie de la communauté scientifique.

Mettant à profit cette nouvelle crédibilité, Bode poussa à la recherche de la planète intermédiaire manquante (n = 4), ce qui conduisit à la découverte de (1) Cérès, astéroïde reclassé en 2006 en planète naine. Urbain Le Verrier et John Couch Adams utilisèrent ensuite cette loi comme première hypothèse pour la distance de la planète hypothétique Neptune, imaginée pour expliquer les perturbations d'Uranus. La valeur de 38,8 prédite par la loi est cependant assez mauvaise et correspond plutôt à l'orbite de Pluton (également considérée comme une planète naine depuis 2006).

Au-delà de Neptune

Objet	Demi- grand axe	Périhélie	Aphélie	Excentricité
Pluton	39,48	29,65	49,31	0,25
Sedna	525,86	76,25	975,47	0,86
Éris	67,67	37,83	97,51	0,44

Les objets supplémentaires découverts après Pluton firent l'objet de tentatives d'intégration dans la loi de Titius-Bode. Certains partisans de la loi de Titius-Bode s'enthousiasmèrent en soulignant qu'avec une distance de 76,1 au, Sedna se trouvait exactement là où la loi prédisait la dixième planète. Toutefois, cette distance correspond dans les faits au périhélie, alors que le demi-grand axe de Sedna vaut environ 515 au. Jusqu’ici, c'était plutôt le demi-grand axe qui servait de référence, et jamais un objet dont la distance au Soleil variait autant n'avait été inclus.

Hypothèses sur le passé du Système solaire

La loi de Titius-Bode a une exception claire, Neptune/Pluton, et un résultat ambigu, la ceinture d'astéroïdes.

Les partisans de la loi de Titius-Bode proposèrent de considérer que la loi avait été vraie par le passé et qu'une perturbation avait modifié l'agencement des planètes. On proposa^[Qui ?] donc que la ceinture d'astéroïdes fût constituée des débris d'une ancienne planète, Phaéton.

De même, pour résoudre le problème posé par Neptune et Pluton, on proposa^[Qui ?] que Neptune fût anciennement à la place où se trouve actuellement Pluton et que Pluton fût à l'époque sa lune. Différentes hypothèses pouvaient expliquer ce mouvement, par exemple l'action de l'hypothétique étoile Némésis.

Finalement, ces propositions ne tiennent pas. La ceinture d'astéroïdes tout entière ne comprend pas assez de matière pour former une planète. Quant à Neptune, les travaux d'analyse sur le passé du Système solaire ont montré qu'elle se trouvait autrefois non pas plus loin du Soleil, mais beaucoup plus près, plus proche même qu'Uranus, qui elle-même était plus proche que sa position actuelle.

Il apparaît donc que la loi de Titius-Bode n'est pas un bon instrument pour étudier le passé de notre système. De plus, la principale piste d'explication de cette loi est de montrer qu'elle génère un système stable. Il n'est donc pas cohérent de supposer qu'elle ait été plus respectée par le passé que maintenant.

Corps célestes supplémentaires

Il a toujours été tentant de chercher à extrapoler les positions de planètes hypothétiques à partir de la loi de Titius-Bode. D'une certaine manière, la loi avait prédit la distance de Pluton, mais l'existence de Neptune semble être une anomalie à cette loi.

La découverte d'objets transneptuniens importants pose tout de même problème à cette loi. D'abord, parce qu'il est difficile de choisir quels objets classer. D'ailleurs, Pluton ayant été rayée de la liste des planètes à la suite de l'écriture d'une définition précise d'une planète, la loi perd sa valeur prédictive. Ensuite, contrairement aux huit planètes, les nouveaux objets découverts suivent une orbite elliptique très différente d'un cercle. Il devient impossible de parler de « distance », et on trouve des résultats correspondant plus ou moins à la loi de Titius-Bode selon qu'on retienne le grand axe ou le périhélie.

Le déclassement de Pluton n'a pas découragé tous les extrapolateurs, certains continuant à mentionner l'existence possible d'une planète majeure à la distance « suivante » selon la loi de Titius-Bode. La majorité des astronomes estiment qu'un objet méritant le nom de planète suivant la nouvelle définition aurait déjà été repéré.

Statut actuel

De nos jours, les astronomes regardent la loi de Titius-Bode comme une curiosité, sans être un mystère majeur de la physique. Il y a débat entre ceux qui pensent que le nombre trop faible d'objets impliqués et la forme arbitraire de la loi permettent de conclure à une simple coïncidence, et ceux qui pensent qu'il reste une explication à chercher. En effet, le fait que la loi cesse d'être vraie à une certaine distance ne veut pas forcément dire qu'il n'y a pas d'explication à chercher — il faut simplement rendre compte de cette limite.

Les dernières théories expliquent la formation des planètes comme la conséquence de mécanismes de résonance qui créeraient des zones orbitales stables lors de la création des systèmes stellaires. Or l'existence de ces configurations stables implique une diminution des axes de liberté du système planétaire. Il est donc alors probable de trouver une loi liant les périhélies. Une loi comme celle de Titius-Bode pour notre système planétaire, mais qui ne s'appliquerait peut être pas dans les autres.

En l'absence d'explication théorique incontestée, le débat demeure. Si le phénomène peut être inexpliqué sans que cela contredise les lois de la physique, c'est parce que le problème à N corps n'a pas de solution analytique exacte. Donc, même si on connaît les lois qui gouvernent les mouvements des planètes, on ne peut pas prédire pour autant avec certitude l'agencement qu'elles doivent adopter.

C'est pour cela que New Scientist ne considère pas cette loi comme un mystère majeur du Système solaire. En comparaison, le fait que la Lune et le Soleil ont le même diamètre apparent depuis la Terre a été classé comme tel.

Autres lois

Le Mysterium Cosmographicum de Kepler.

Dès 1596, dans le Mysterium Cosmographicum, Johannes Kepler construit un modèle géométrique des rayons relatifs des orbites planétaires. Chacun des cinq solides de Platon s'intercale entre deux des six planètes connues à l’époque (de Mercure à Saturne); chaque orbite est circonscrite au polyèdre intérieur et est inscrite dans le polyèdre extérieur.

Otto Schmidt a proposé d'appliquer une fonction pour les planètes telluriques et une autre pour les planètes gazeuses.

La loi de Dermott traite, quant à elle, des satellites de Jupiter et a été adaptée pour ceux de Saturne, Uranus et Neptune. Des lois similaires, de type puissance ou exponentielle, ont également été proposées pour certains systèmes planétaires extrasolaires.

Voir aussi

Bibliographie

• [Lequeux 2009] James Lequeux, Le Verrier : savant magnifique et détesté, Les Ulis et Paris, EDP Sciences et l'Observatoire de Paris, coll. « Sciences et histoires », juin 2009, 1^re éd., V-401 p., ill. et portr. (ISBN 978-2-7598-0422-1 et 978-2-901057-61-1, EAN 9782759804221, OCLC 470959777, BNF 41475583, SUDOC 134069129, présentation en ligne, lire en ligne), chap. 2, encadré 2.1 (« La loi de Titius-Bode »), p. 24.

Articles connexes

• histoire de l'astronomie
• harmonie des sphères

Liens externes

• [audio] Bérangère Dubrulle, Dieu joue-t-il à la pétanque ?, les podcasts de Ciel et Espace radio
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Gran Enciclopèdia Catalana
  • Larousse
  • Store norske leksikon
  • Universalis