Corde (géométrie)
En géométrie, une corde est un segment reliant deux points d’un cercle ou d’une autre courbe.
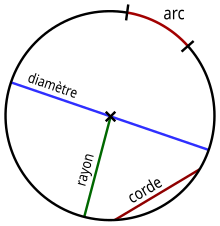
Propriétés des cordes d'un cercle
modifierLongueur
modifierUne corde d'un cercle de rayon interceptant un angle au centre de mesure est de longueur .
Une corde d'un cercle est donc de longueur inférieure à celle du diamètre , avec égalité si et seulement si ses deux extrémités sont diamétralement opposées.
Formule des cordes consécutives : Soient trois points d'un cercle de diamètre , et étant situés de part et d'autre du diamètre issu de . Par application du théorème de Ptolémée, Les longueurs des cordes sont reliées par la relation [1].
La loi de probabilité de la longueur d’une corde dépend de la manière dont sont choisies ses extrémités, ce qui donne lieu au paradoxe de Bertrand.
Théorème des cordes sécantes
modifierÉtant donné un point à l'intérieur d'un cercle de centre et de rayon , toutes les cordes passant par fournissent un produit constant égal à . C'est l'opposé de la puissance de par rapport au cercle.
Théorème de l'angle inscrit
modifierÉtant donné une corde d'un cercle de centre , tous les angles pour des points du cercle situés du même côté de la corde ont même mesure, égale à .
L'angle de droites est même constant pour tout point du cercle.
On en déduit le théorème de l'angle entre deux cordes sécantes indiqué dans la figure de droite.
Problèmes de partage
modifierDénombrement
modifierÉtant donnés n points distincts sur un cercle, les cordes qui relient ces points partagent le disque en au plus composantes connexes[2], soit [3],[4],[5],[6],[7],[8],[9]:
- .
Cette formule est la solution du problème du cercle de Moser[10]. Elle coïncide avec les premières puissances de 2 jusqu’au rang n = 5, mais diffère ensuite[3]. Les nombres sont ceux de la colonne 4 du triangle de Bernoulli.
Théorème de la pizza
modifierCe théorème propose des partages équitables d'un disque par des cordes concourant en un point autre que le centre.
Quadrisection
modifierLe problème du partage du disque en quatre parties de même aire par des cordes issues de la circonférence ou des cordes parallèles fait intervenir le nombre de Dottie.
Diagrammes de cordes
modifierLes cordes d'un cercle permettent de définir les diagrammes de cordes ou diagrammes de Gauss, utiles notamment en théorie des nœuds.
Corde d'une courbe représentative de fonction
modifierÉtant donné une fonction réelle définie sur un intervalle , la corde reliant les points de coordonnées et a pour équation
- .
Son coefficient directeur est le taux d'accroissement de la fonction entre les valeurs a et b.
Cette corde réalise ainsi une approximation affine de la fonction par interpolation.
Notes et références
modifier- Yves Ladegaillerie, Géométrie, Ellipses, , p. 359
- Illustration du phénomène et démonstration, sur le site de Gérard Villemin.
- Voir la suite A000127 de l'OEIS.
- (en) Ivan Niven, Mathematics of Choice, MAA, (lire en ligne), p. 195, solution du problème 40 (posé p. 158).
- (en) « Maximal number of regions obtained by joining n points around a circle by straight lines », sur OEIS
- Alain Bouvier, La mystification mathématique, Hermann, , p. 37-39
- John H. Conway, Richard K. Guy, Le livre des nombres, Eyrolles, , p. 76-79
- (en) Marc Noy, « A Short Solution of a Problem in Combinatorial Geometry », Mathematics Magazine, , p. 52 (lire en ligne)
- (en) Richard K. Guy, « The Strong Law of Small Numbers », American Mathematical Monthly, vol. 95, no 8, , p. 697–698,706 (ISSN 0002-9890, DOI 10.2307/2322249, JSTOR 2322249, lire en ligne)
- Voir par exemple la vidéo The absurd circle division pattern (updated) | Moser's circle problem de Grant Sanderson (3Blue1Brown)
Voir aussi
modifier- Le théorème des globes oculaires, concernant des cordes de deux cercles disjoints.
- Le théorème des sept cercles, énonçant le concours de cordes associées à ces cercles.
- Le théorème du papillon, concernant trois cordes concourantes d'un cercle, le point de concours étant le milieu de l'une d'entre elles.
- Le théorème de la corde universelle, énonçant les conditions d'existence pour les courbes paramétrées joignant à d'une corde parallèle à .