Cocoloration

En théorie des graphes, une cocoloration d'un graphe G est une affectation de couleurs aux sommets de telle sorte que chaque classe de couleur forme un ensemble indépendant dans G ou dans le graphe complémentaire de G. Le nombre cochromatique z( G ) de G est le plus petit nombre de couleurs nécessaires dans une cocoloration de G. Les graphes de nombre cochromatique 2 sont exactement les graphes bipartis, les compléments des graphes bipartis et les graphes divisés.

Cocoloration avec 3 couleurs (figure en haut à gauche) : une 3-coloration propre de ce graphe est impossible. Le sous-graphe bleu forme une clique (figure en bas à droite), tandis que les sous-graphes rouge et vert forment des cliques du graphe complémentaire.

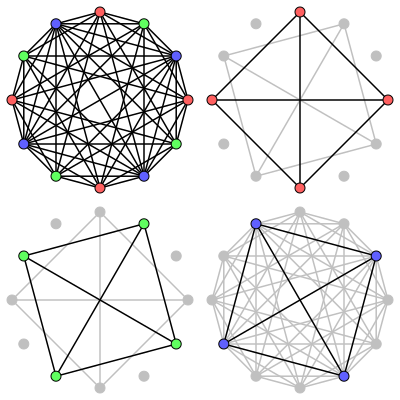
Comparaison

La condition que chaque classe de couleur est une clique ou est un ensemble indépendant est plus faible que la condition de la coloration (où chaque classe de couleur doit être un ensemble indépendant) et est plus forte que pour la sous-coloration (en) (où chaque classe de couleur doit être une union disjointe de cliques) ; il s'ensuit que le nombre cochromatique de G est inférieur ou égal au nombre chromatique de G, et qu'il est supérieur ou égal au nombre sous-chromatique de G.

Historique

La cocoloration a été nommée et étudiée pour la première fois par Lesniak et Straight (1977). Jørgensen (1995) caractérise des graphes trichromatiques critiques, tandis que Fomin, Kratsch et Novelli (2002) décrivent des algorithmes permettant d'approcher le nombre cochromatique d'un graphe. Zverovich (2000) définit une classe de graphes cochromatiques parfaits, analogue à la définition de graphes parfaits via la coloration de graphes, et fournit une caractérisation de sous-graphe interdite de ces graphes.

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « cocoloring » (voir la liste des auteurs).