Point d'arrêt (mécanique des fluides)
En mécanique des fluides, un point d’arrêt (ou point de stagnation) est un point de l’écoulement d'un fluide sur un corps où la vitesse locale des particules du fluide est amenée à zéro du fait des symétries. Ce point d'arrêt fait face à l'écoulement et on peut le voir, pour un corps 3D, comme le point où s'écrasent les particules qui n'ont pu contourner le corps ni par le haut ni par le bas, ni par la gauche ni par la droite. Pour un corps 2D comme une aile, on peut voir le point d'arrêt comme le point où s'écrasent les particules qui ne passent ni au-dessus du corps ni au-dessous.
Sur l'image ci-dessous (celle d'un corps de révolution hémisphéro-cylindrique) on peut observer l'évolution des coefficients de pression (représentés en ordonnées et en fuchsia) au long de l'axe de révolution du corps : à l'approche du corps les particules se déplaçant sur cet axe sont peu à peu freinées jusqu'à la vitesse nulle (au point d'arrêt) de sorte qu'en application du Théorème de Bernoulli le coefficient de pression locale passe de (loin du corps) à l'unité au point d'arrêt (vitesse nulle).
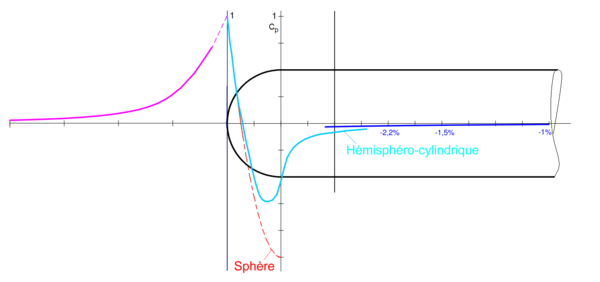
Le point d'arrêt
modifierEn aérodynamique le corps n'existe qu'au travers des conditions qu'il impose à l'écoulement. Le point d'arrêt est donc un point de l'écoulement et non du corps. Il correspond à une singularité liée aux symétries qui peuvent être de deux types :
- une symétrie de révolution (par exemple liée à un objet sphérique) qui entraîne la présence d'un point singulier au voisinage de l'intersection du corps et de l'axe de symétrie : le point d'arrêt ;
- une symétrie plane (par exemple un cylindre infini perpendiculaire à l'écoulement) qui entraîne la présence d'une ligne singulière : la ligne d'arrêt. Dans ce cas la représentation du problème dans un plan fait que la ligne se réduit à un point et l'on parle abusivement de « point d'arrêt ».
Dans le cas de deux plans de symétrie perpendiculaires (par exemple un ellipsoïde) chaque plan génère une ligne de singularité de la composante de l'écoulement qui lui est perpendiculaire ; l'intersection des deux lignes constitue le point d'arrêt. Tout corps régulier peut être représenté localement par un ellipsoïde (plutôt que par le plan tangent, les courbures jouant un rôle en aérodynamique).
Le plan est une géométrie qui entraîne les effets précédents :
- ligne d'arrêt pour un écoulement en incidence (un seul plan de symétrie) ;
- point d'arrêt pour un écoulement normal au plan (axe de symétrie).
Le point d'arrêt est un point à vitesse nulle. En effet :
- la symétrie du problème (liée aux symétries de l'objet) impose la symétrie de la solution (de l'écoulement). , définissant la ligne d'arrêt (normale, suivant le problème, à la droite tangente ou au plan tangent à la surface au point d'arrêt) et (ou ) définissant le point d'arrêt. Donc , et désignant le voisinage mathématique de 0 ;
- la continuité (conservation de la masse) impose la dérivabilité de en tout point (on exclut les ondes de choc) et en particulier V est continue en .
est une fonction continue symétrique autour de l'origine : elle est donc nulle en 0. au point d'arrêt est donc la conséquence de la symétrie, dans le cadre des équations (Navier-Stokes ou Euler) qui imposent la continuité de V. On remarque que ceci n'impose pas la continuité de sa dérivée, ce qui est effectivement le cas de tous les écoulements de point d'arrêt qui ont une accélération non nulle. C'est la raison pour laquelle le plan n'est pas une bonne approximation locale d'une surface en aérodynamique.
Pression au point d'arrêt (ou pression d'arrêt)
modifierAu point d'arrêt, la vitesse du fluide est nulle et toute l'énergie cinétique de ce fluide est transformée en énergie de pression de façon isentropique.
L’application du théorème de Bernoulli indique que la pression statique est la plus forte lorsque la vitesse est nulle. Dans le cas d’un écoulement incompressible, cela signifie que le coefficient de pression au point d’arrêt est égal à .
En effet, pour les gaz, la variante adimensionnelle de l’équation de Bernoulli s’écrit :
Cp étant le coefficient de pression et Cv étant le coefficient de vitesse. Par définition, le coefficient de vitesse Cv vaut :
- , étant la vitesse locale et la vitesse à l’infini loin du corps.
Lorsque l’on pose (donc ) dans cette équation, on observe que .
Par définition, le coefficient de pression au point de stagnation est donné par :
où :
- est la pression statique au point où la mesure est effectuée ;
- est la pression statique loin du corps testé ;
- est la pression dynamique loin du corps testé.
c’est-à-dire :
- donc pour , la pression locale vaut
Le coefficient de pression au point d’arrêt égale 1[1].
Cela signifie qu'au point d’arrêt, la pression statique locale (nommée Pression d'arrêt) vaut la somme de la pression statique à l’infini (pression ambiante ou atmosphérique) et de la pression dynamique .
La pression dynamique est ainsi nommée parce qu'elle est la surpression due au mouvement relatif du corps par rapport au fluide.
À l'amont de certains corps 2D présentés en travers d'un écoulement de fluide on constate l'existence d'une ligne d'arrêt de unitaires.
La galerie d'images ci-dessous montre la distribution des coefficients de pression sur un certain nombre de corps. L'écoulement sur tous ces corps venant de la gauche, on doit rechercher le au point d'arrêt à l’extrême gauche des courbes du .
Les mécaniciens des fluides sont tellement conscients que le au point d'arrêt est unitaire qu'ils ne le dessinent pas toujours (comme sur la courbe rouge de la deuxième image)[Note 1] :
-
Distribution des pressions (Cp) sur la sphère à plusieurs nombres de Reynolds, d'après Achenbach.
-
Distribution des autour du dirigeable Akron.
-
Distribution des dans le plan de symétrie d'un berline routière DrivAer Fastback.
-
Distribution des pressions sur le cône d'Apollo (module de commande) à l'incidence zéro.
Limitation de la loi la valeur de la pression dynamique au point d'arrêt
modifier- Dépendance du nombre de Reynolds :
Pour les très faibles nombres de Reynolds (Reynolds basé sur le diamètre du corps, par exemple, pour un corps de révolution) une pression visqueuse doit être ajouté à la pression due à l'inertie[2], ce qui donne à la pression au point d'arrêt une valeur de l'ordre de , ce étant basé sur le diamètre du corps. Au-dessus du Reynolds 3000, par contre, (Reynolds toujours basé sur le diamètre du corps) la Pression dynamique au point d'arrêt est bien [3].
- Dépendance du nombre de Mach :
Par raison de simplification, dans beaucoup de calculs subsoniques l’air est considéré comme incompressible, mais il est évidemment compressible. Pour l’air au niveau de la mer aux faibles valeurs de Mach, l’erreur relative sur le est assimilable à . On peut donc mémoriser que dès , l’erreur sur le est de 1 %[4],[Note 2].
Notes et références
modifierNotes
modifier- De même, la courbe bleue de cette image n'indique pas le coefficient de vitesse nul, au point d'arrêt du corps.
- 1 % est une erreur négligeable. Selon les cas, on peut donc considérer que l'air est incompressible jusqu'à ou
Références
modifier- (en) L. J. Clancy, Aerodynamics, Pitman Publishing Limited, London, 1975, Section 3.6
- Zahm A.F., Pressure of air on coming to rest from various speeds, NACA Report, no 247.
- E. Ower et F. C. Johansen, On a Determination of the Pitot-Static Tube Factor at Low Reynolds Numbers, with Special Reference to the Measurement of Low Air Speeds, 1931.
- Pierre Rebuffet, Aérodynamique expérimentale, 1962, Librairie Polytechnique Ch. Béranger, Paris, ouvrage essentiel, non réédité.

