Courbure de champ
- Ne doit pas être confondu avec la correction flat-field, qui fait référence à la correction de la sensibilité lumineuse des pixels d'un capteur CCD.
La courbure de champ de Petzval ou CCP, nommée d'après Joseph Petzval, est un type d'aberration optique.
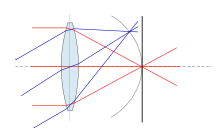
Lorsqu’un système optique présente de la courbure de champ, l’image d’un plan se focalise sur une portion de sphère. La majorité des capteurs étant plans, l’aberration induit une défocalisation partielle qui se traduit par une zone floue dans l’image.
La courbure de champ est une aberration à symétrie de révolution autour de l’axe optique. Elle augmente de manière quadratique avec le champ.
Observation du phénomène
modifierLa courbure de champ correspond à un défaut de mise au point qui varie avec le carré de la distance à l'axe optique[1]. L’image d’un plan n’est donc plus un plan, mais une portion de sphère.
La plupart des détecteurs (écrans, films, CCD...) étant plans, seule l’intersection entre la sphère image et le plan du détecteur sera nette. En pratique, les images produites sont floues dans les coins et le centre net, ou l’inverse, en fonction de la mise au point choisie.
Développement polynomial de la courbure de champ
modifierPolynôme de Seidel associé
modifierDans le formalisme de Seidel, la courbure de champ s'exprime de la manière suivante:
Avec Δ l'écart normal et y la distance entre le point image et l’axe optique.
On retrouve bien dans cette expression l'évolution quadratique du défocus avec .
Polynôme de Zernike associé
modifierDans le formalisme de Zernike, la courbure de champ et le défocus s'expriment dans le même polynôme .
Somme de Petzval
modifierLa courbure de champ de Petzval d'un système optique est égale à la somme de Petzval,
où est le rayon de la ième surface et les n sont les indices de réfraction de la première et de la seconde face de la surface[2].
Courbure de Petzval et astigmatisme
modifierDans le cas où le système optique présente de l'astigmatisme, la courbure de Petzval est donnée par la moyenne des courbures de champ de la composante sagittale et de la composante tangentielle[3].
Exemples de domaines concernés
modifierPhotographie argentique
modifierLa plupart des objectifs photographiques actuels sont conçus pour minimiser la courbure de champ, et ont donc une distance focale qui s'accroît en fonction de l'angle du rayon optique. Cependant, certains appareils photo argentiques avaient leur presse-film courbé pour compenser le phénomène, en particulier quand l'objectif était fixe et connu. Cela permettait de minimiser les défauts des optiques rudimentaires (ménisque) d'appareils bon marché. Ceci incluait également les plans-films, qui pouvaient également être légèrement courbés.
Photographie numérique
modifierLes capteurs numériques ne peuvent généralement pas être pliés, bien que les grands réseaux de capteurs (de toute façon nécessaires du fait de la taille limitée des puces) puissent être mis en forme pour simuler une surface courbe (surface focale). Pourtant l'intérêt d'un capteur courbe a poussé Sony à produire un CMOS incurvé en 2014[4].
Astronomie
modifierCorrection de la courbure de champ
modifierAfin de compenser l'effet de la courbure de champ, il est envisageable de :
- donner la même courbure au détecteur (CCD, CMOS, film photographique) ;
- conserver un détecteur plan mais corriger la courbure de champ par une méthode optique ou numérique.
Par des procédés optiques
modifierPour compenser de manière optique la courbure de champ, il est possible d'ajouter à la surface du détecteur un système optique simple (lentille, doublet ou triplet) appelé aplanisseur de champ qui modifie le moins possible l'image formée mais redresse le front d'onde.
Par du traitement d'image
modifierNotes et références
modifierRéférences
modifier- Introduction to Optical Testing sur Google Livres
- A History of the Photographic Lens sur Google Livres
- Elements de Conception Optique sur Google Livres
- Rishi Sanyal, « Sony's curved sensors may allow for simpler lenses and better images », sur dpreview.com, (consulté le ).