Courbe du blanc-manger

En mathématiques, la courbe du blanc-manger est une courbe fractale constructible par subdivision de son ensemble de définition. Elle est aussi connue comme la courbe de Takagi, d'après Teiji Takagi qui l'a décrite en 1901, ou comme la courbe de Takagi-Landsberg (en), une généralisation de la courbe. Le nom blanc-manger vient de sa ressemblance à l'entremets du même nom. C'est un cas particulier de courbe de De Rham (en).

Courbe du blanc-manger ou "de Tagaki"

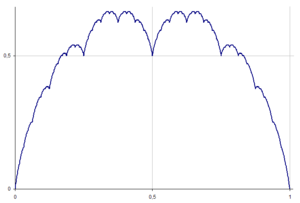
Définition

La fonction blanc-manger est définie sur ℝ par : ${\rm {blanc}}(x)=\sum _{n=0}^{+\infty }{s(2^{n}x) \over 2^{n}}$, où s est définie par $s(y)=\min _{n\in {\mathbb {Z} }}|y-n|$, c'est-à-dire que s(y) est la distance entre y et l'entier relatif le plus proche.

La série de fonctions définissant blanc(x) pour tout nombre x est normalement convergente donc la fonction blanc-manger est continue (et 1-périodique, donc uniformément continue), mais elle n'est dérivable en aucun point . Sa courbe représentative est une fractale (c'est l'attracteur d'un système de fonctions itérées).

La courbe de Takagi–Landsberg en est une généralisation donnée par la relation : $T_{w}(x)=\sum _{n=0}^{+\infty }w^{n}s(2^{n}x)$ pour un paramètre w. La valeur H = –log₂w est appelée le « paramètre de Hurst ».

La courbe du blanc-manger est donc le cas w = 1/2, c'est-à-dire H = 1.

Construction graphique

La courbe du blanc-manger peut être construite à partir des fonctions en dents de scie si la série est approchée par les premiers termes. Sur les illustrations ci-dessous, les fonctions en dents de scie (en rouge) sont progressivement ajoutées à la courbe à chaque étape.

• 

  n = 0

• 

  n ≤ 1

• 

  n ≤ 2

• 

  n ≤ 3

Primitive de la fonction

Étant donné que l'intégrale de 0 à 1 de la fonction blanc vaut 1/2, la relation ${\rm {blanc}}(x)={\rm {blanc}}(2x)/2+s(x)$ permet de calculer la primitive I s'annulant en 0 : $I(x)=\int _{0}^{x}{\rm {blanc}}(t)\,{\rm {d}}t.$

Le calcul est récursif et son temps de calcul est de l'ordre du logarithme de la précision requise. $I(x)={\begin{cases}1/2+I(x-1)&{\text{si }}x\geq 1\\1/2-I(1-x)&{\text{si }}1/2<x<1\\I(2x)/4+x^{2}/2&{\text{si }}0\leq x\leq 1/2\\-I(-x)&{\text{si }}x<0.\end{cases}}$

Dimension fractale

La courbe de Takagi-Landsberg de paramètre de Hurst H a pour dimension de Hausdorff 2 – H.

La dimension de Hausdorff de la courbe du blanc-manger, pour laquelle H = 1, vaut donc 1, malgré son aspect fractal.

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Blancmange curve » (voir la liste des auteurs).

Voir aussi

Articles connexes

• Fonction de Bolzano
• Fonction de Weierstrass
• Fonction continue nulle part dérivable

Liens externes

• Takagi Explorer
• Les courbes de Weierstrass et La courbe de Bolzano

Article

• (en) Teiji Takagi, « A Simple Example of the Continuous Function without Derivative », Proc. Phys.-Math. Soc. Jpn., vol. 1,‎ 1901, p. 176–177 (DOI 10.11429/subutsuhokoku1901.1.F176)