Année tropique
L'année tropique, ou année équinoxiale ou encore année solaire, correspond à la périodicité des saisons terrestres : elle est définie comme l'intervalle de temps au bout duquel la position apparente du Soleil vue de la Terre, définie par la longitude moyenne du Soleil sur son orbite apparente (voir écliptique), revient à la même valeur. C'est la durée moyenne qui sépare le commencement des différentes saisons.
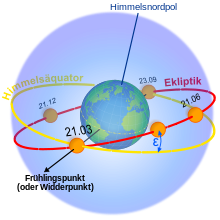
Cette notion de durée moyenne est importante, car la vitesse de la Terre sur son orbite n’est pas uniforme, car cette dernière est une ellipse. Cette vitesse obéit en première approximation à la seconde loi de Kepler, mais en réalité le temps moyen mis pour aller d’un équinoxe de printemps à l’autre n’est pas strictement égal au temps moyen qui sépare deux équinoxes d’automne et il en est de même pour les solstices d’hiver et d’été. L'ancienne définition de l'année tropique qui était simplement la durée séparant deux équinoxes de printemps (passage au point vernal) s'appelle désormais l'année vernale. On doit cette définition moderne moyennée de l'année tropique à l'astronome André Danjon[réf. nécessaire].
L'année tropique est également différente du temps que met la Terre pour effectuer une orbite complète autour du Soleil par rapport à un repère constitué d'étoiles fixes lointaines, qui constitue l'année sidérale. L'écart entre les deux (environ 20 minutes) est la mesure de la précession des équinoxes.
Étymologie modifier
Le mot « tropique » vient du bas latin tropicus, lui-même issu du mot grec tropikos, de tropos « tour, changement ».
Durée modifier
La durée de l'année tropique varie en fonction de l'époque. Selon la dernière théorie VSOP2013 (polynôme du sixième degré reproduit ci-dessous)[1], elle diminue régulièrement, soit actuellement d'environ 0,528 50 s par siècle (écart pour la période du au ), ou d'environ 0,005 284 s par an (moyenne sur la période du au ), pour théoriquement augmenter à partir du (accroissement alors de 0,014 s par siècle). Jusqu'à récemment, l’Institut de mécanique céleste et de calcul des éphémérides (IMCCE) évaluait l'année tropique selon la théorie semi-analytique des planètes VSOP2000 ; pour le , 12 h UTC, le calcul donnait une durée de 365 jours 5 heures 48 minutes 45,260 634 2 secondes[2], soit 31 556 925,260 634 2 s ou 365,242 190 516 6 jours standards de 24 heures. Dans une publication datée de septembre 2021, l’IMCCE a révisé cette valeur, dorénavant estimée, selon la nouvelle théorie VSOP2013, à 365,242 190 448 2 jours, soit 365 jours 5 heures 48 minutes 45,254 724 5 s[1], toujours au , 12 h UTC.
Voici une expression que donnait, jusqu'à récemment, la théorie semi-analytique des planètes VSOP2000 par un développement limité au 4e degré:
- 365,242 190 516 6 – Tk × 0,000 061 560 – Tk2 × 0,000 000 068 4 + Tk3 × 0,000 000 263 0 + Tk4 × 0,000 000 003 2,
où Tk est donné en millier d'années de 365,25 jours par rapport à l'année 2000.0, soit Tk = ((JJ - 2 451 545) / 365 250), où JJ est le jour julien.
La formule peut être calculée plus simplement avec moins de décimales pour les puissances sous la forme :
- 365,242 190 516 6 – TM × 0,061 560 – TM2 × 0,068 4 + TM3 × 263,0 + TM4 × 3 200,
où TM = Tk / 1000 est donné en million d'années de 365.25 jours par rapport à l'année 2000.0, soit TM = ((JJ - 2 451 545) / 365 250 000), où JJ est le jour julien.
Ci-dessous, on trouvera la nouvelle expression, plus précise, que donne la théorie semi-analytique des planètes VSOP2013[1]:
365,242 190 448 2 – Tk × 0,000 061 166 23 – Tk2 × 0,000 000 065 922 + Tk3 × 0,000 000 266 790 9 + Tk4 × 0,000 000 000 947 396 + Tk5 × 0,000 000 000 106 233 + Tk6 × 0,000 000 000 371 993,
où Tk est donné en millier d'années de 365,25 jours par rapport à l'année 2000.0, soit Tk = ((JJ - 2 451 545) / 365 250), où JJ est le jour julien.
Ce nouveau polynôme du sixième degré donne ainsi, comme valeurs de l'année tropique : 365 jours 5 heures 48 minutes 45,143 738 5 secondes au 1er janvier 2021, 0 h TU (...45,143 731 7 s à 12 h TU) ; 365 jours 5 heures 48 minutes 45,138 457 2 secondes au 1er janvier 2022, 0 h TU (...45,138 45 s à 12 h TU) et 365 jours 5 heures 48 minutes 45,133 175 8 secondes au 1er janvier 2023, 0 h TU (...45,133 168 6 à 12 h TU).
De ces deux polynômes il découle que la durée de l'année tropique oscille avec le temps. Ainsi, le premier polynôme de degré quatre fait apparaître 3 extremums locaux, soit un minimum local estimé dans la préhistoire (vers le milieu de l'an -57 964), un maximum local dans l'antiquité et un minimum projeté dans le futur d'après les mesures actuelles. Selon ce polynôme du 4e degré, le dernier maximum a été atteint en l'an -7 503 avec 365,242 569 738 1 jours (soit 365 jours 5 heures 49 minutes 18,025 37 secondes) et le prochain minimum le sera en l'an 10 365 avec 365,241 840 389 8 jours (soit 365 jours 5 heures 48 minutes 15,009 68 secondes) ; on voit que la différence entre ces extrêmes est de 0,000 729 348 3 jours, soit 63,015 69 secondes. La formule cependant ne permet pas une aussi grande précision hors de la période de ces extremums (avant l'an -7502 ou après l'an 10365), car elle diverge ensuite rapidement vers l'infini au-delà et ne peut pas tenir compte de certains événements astronomiques inconnus comme les éruptions solaires, ni de la variation irrégulière de la rotation terrestre causée par des phénomènes géologiques dont on ne sait pas prédire avec précision l'importance sur des périodes aussi longues échappant à l'histoire humaine.
Les cautèles ci-dessus se justifient d'autant plus lorsque l'on analyse le nouveau polynôme de degré six développé avec la théorie VSOP2013. En effet, ce nouveau polynôme, contrairement au précédent de la théorie VSOP2000, ne présente plus de maximum, mais seulement une unique valeur minimale. Cette dernière est égale, selon le logiciel d'accès libre Maxima, à 365,241 894 327 373 700 956 020 294 666 877 574 jours, soit environ 365 jours 5 heures 48 minutes 19,669 885 087 762 600 secondes, valeur qui sera théoriquement atteinte le jour julien 4829416,719 363 199 948 628 598 101, soit le 24 mai de l'an 8510, à 5h 15m 52,980 475 7 secondes TU.
Concernant la valeur de 365,2422 jours (à moins de 0,825 seconde près de la valeur pour 2000.0 du polynôme de degré six et à 31 secondes de chacun des extrêmes du polynôme de degré quatre) parfois employée pour l'année tropique, on peut noter qu'il s'agit là de la valeur moyenne arrondie entre les extrêmes du polynôme de degré quatre, observation qui n'a toutefois plus de pertinence s'agissant du nouveau polynôme de degré six, comme expliqué plus haut. Il existe un léger écart d'environ 26 secondes avec l'année calendaire de l'ère commune (année grégorienne), qui présente une valeur moyenne un peu plus forte de 3/10 000, soit une durée de 365,2425 jours exactement depuis 1582, année d'adoption du calendrier grégorien. Le retard du calendrier grégorien avec l'année tropique moyenne serait donc de 3 jours en 10 000 ans. Le retard du calendrier julien (l'année julienne ayant une valeur moyenne encore plus élevée de 365,25 jours exactement) serait de 78 jours avec l'année tropique et de 75 jours avec le calendrier grégorien. Mais, pour être complet, il faudrait aussi tenir compte du ralentissement continu et inéluctable de la rotation de la Terre, qui ajoutera encore au moins 3 jours d'écart d'ici là.
Bibliographie modifier
- (en) Jean Meeus et D. Savoie, « The history of the tropical year », Journal of the British Astronomical Association, vol. 102, no 1, , p. 40–42 (résumé, lire en ligne) et aussi Jean Meeus, « More Mathematical Astronomy Morsels » (i.e. Morsels II), Willmann-Bell, Inc. 2002, p. 357-366
- Fabienne Casoli, L'astronomie, Minerva, , p. 32-33
- (en) K. M. Borkowski, « The tropical year and the solar calendar », Journal of the Royal Astronomical Society of Canada, vol. 85, no 3, , p. 121–130 (lire en ligne)
- Nathalie Audard, Gilles Carnal, Bastien Confino et al., Astronomie, Hachette Collections, , p. 9-10
- Institut de mécanique céleste et de calcul des éphémérides (Jérôme Berthier, Pascal Descamps, François Mignard ), Observatoire de Paris, Observatoire de la Côte d’Azur et Bureau des longitudes, Introduction aux éphémérides et phénomènes astronomiques, EDP Sciences, , p. 864-873
Notes et références modifier
- IMCCE Introduction aux éphémérides et phénomènes astronomiques
- IMCCE Institut de nécanique céleste et de calcul des éphémérides "L'année tropique" Site Internet: ftp://ftp.imcce.fr/pub/misc/annee_tropique/annee_tropique.doc