Loi inverse-gaussienne

Loi inverse-gaussienne
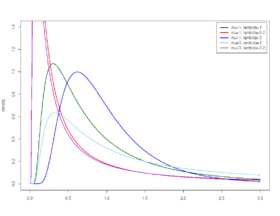Densité de probabilité
Paramètres	$\lambda >0$ $\mu >0$
Support	$x\in ]0,\infty [$
Densité de probabilité	$\left[{\frac {\lambda }{2\pi x^{3}}}\right]^{1/2}\exp {\frac {-\lambda (x-\mu )^{2}}{2\mu ^{2}x}}$
Fonction de répartition	$\Phi \left({\sqrt {\frac {\lambda }{x}}}\left({\frac {x}{\mu }}-1\right)\right)$ $+\exp \left({\frac {2\lambda }{\mu }}\right)\Phi \left(-{\sqrt {\frac {\lambda }{x}}}\left({\frac {x}{\mu }}+1\right)\right)$ où $\Phi \left(\right)$ est la fonction de répartition de la loi normale
Espérance	$\mu$
Mode	$\mu \left[\left(1+{\frac {9\mu ^{2}}{4\lambda ^{2}}}\right)^{\frac {1}{2}}-{\frac {3\mu }{2\lambda }}\right]$
Variance	${\frac {\mu ^{3}}{\lambda }}$
Asymétrie	$3\left({\frac {\mu }{\lambda }}\right)^{1/2}$
Kurtosis normalisé	${\frac {15\mu }{\lambda }}$
Fonction génératrice des moments	$e^{\left({\frac {\lambda }{\mu }}\right)\left[1-{\sqrt {1-{\frac {2\mu ^{2}t}{\lambda }}}}\right]}$
Fonction caractéristique	$e^{\left({\frac {\lambda }{\mu }}\right)\left[1-{\sqrt {1-{\frac {2\mu ^{2}\mathrm {i} t}{\lambda }}}}\right]}$

En théorie des probabilités et en statistique, la loi inverse-gaussienne (ou loi gaussienne inverse ou encore loi de Wald) est une loi de probabilité continue à deux paramètres et à valeurs strictement positives. Elle est nommée d'après le statisticien Abraham Wald.

Le terme « inverse » ne doit pas être mal interprété, la loi est inverse dans le sens suivant : la valeur du mouvement brownien à un temps fixé est de loi normale, à l'inverse, le temps en lequel le mouvement brownien avec une dérive positive (drifté) atteint une valeur fixée est de loi inverse-gaussienne.

Sa densité de probabilité est donnée par

$f(x;\mu ,\lambda )={\begin{cases}\displaystyle \left({\frac {\lambda }{2\pi x^{3}}}\right)^{1/2}\exp {\frac {-\lambda (x-\mu )^{2}}{2\mu ^{2}x}}&{\text{ pour }}x>0,\\0&{\text{ sinon}}.\end{cases}}$

où μ > 0 est son espérance et λ > 0 est un paramètre de forme.

Lorsque λ tend vers l'infini, la loi inverse-gaussienne se comporte comme une loi normale, elle possède plusieurs propriétés similaires avec cette dernière.

La fonction génératrice des cumulants (logarithme de la fonction caractéristique) de la loi inverse-gaussienne est l'inverse de celle de la loi normale.

Pour indiquer qu'une variable aléatoire X est de loi inverse-gaussienne de paramètres $\mu$ et $\lambda$, on utilise la notation $X\sim IG(\mu ,\lambda ).\,\!$

Propriétés

Somme

Si les variables aléatoires $X_{i}$, $i=1,2,\dots ,n$ ont pour loi $IG(\mu _{0}w_{i},\lambda _{0}w_{i}^{2})$ respectivement, et sont indépendantes, alors leur somme est de loi inverse-gaussienne :

$S=\sum _{i=1}^{n}X_{i}\sim IG\left(\mu _{0}\sum w_{i},\lambda _{0}\left(\sum w_{i}\right)^{2}\right).$

Il est à remarquer que

${\frac {{\textrm {Var}}(X_{i})}{{\textrm {E}}(X_{i})}}={\frac {\mu _{0}^{2}w_{i}^{2}}{\lambda _{0}w_{i}^{2}}}={\frac {\mu _{0}^{2}}{\lambda _{0}}}$

est constant pour tout i. C'est une condition nécessaire pour cette formule de sommation.

Échelle

Si X est de loi inverse-gaussienne, alors pour tout t > 0, tX est de loi inverse-gaussienne dont les paramètres sont multipliés par t :

$X\sim IG(\mu ,\lambda )\quad \Longrightarrow \quad tX\sim IG(t\mu ,t\lambda ).$

Famille exponentielle

La loi inverse-gaussienne est une famille exponentielle à deux paramètres avec pour paramètres naturels ${\frac {-\lambda }{2\mu ^{2}}}$ et ${\frac {-\lambda }{2}}$, et pour statistiques naturelles X et 1/X.

Lien avec le mouvement brownien

Le processus stochastique $X=(X_{t},t\geq 0)$ défini par

${\begin{cases}X_{0}=0\\X_{t}=\nu t+\sigma W_{t}\end{cases}}$

où $(W_{t},t\geq 0)$ est le mouvement brownien standard et ν > 0, est un mouvement brownien drifté par ν.

Ainsi, le temps d'atteinte (ou premier temps de passage) de la valeur (ou niveau) α > 0 fixé par X est aléatoire et de loi inverse-gaussienne :

$T_{\alpha }=\inf\{t>0\mid X_{t}=\alpha \}\sim IG\left({\frac {\alpha }{\nu }},{\frac {\alpha ^{2}}{\sigma ^{2}}}\right).\,$

Pour un drift nul

Un cas particulier usuel de l'explication précédente est le cas où le mouvement brownien n'a pas de drift. Dans ce cas, le paramètre μ tend vers l'infini, et le temps d'atteinte d'une valeur α < 0 fixée est une variable aléatoire de densité de probabilité celle de la distribution de Lévy avec paramètre $c={\frac {\alpha ^{2}}{\sigma ^{2}}}$ :

$f\left(x;0,\left({\frac {\alpha }{\sigma }}\right)^{2}\right)={\frac {\alpha }{\sigma {\sqrt {2\pi x^{3}}}}}\exp \left(-{\frac {\alpha ^{2}}{2x\sigma ^{2}}}\right).$

Maximum de vraisemblance

Considérons le modèle donné par

$X_{i}\sim IG(\mu ,\lambda w_{i}),\,\,\,\,\,\,i=1,2,\ldots ,n$

où tous les w_i sont connus, $(\mu ,\lambda )$ sont inconnus et où les variables indépendantes X_i ont pour fonction de vraisemblance :

$L(\mu ,\lambda )=\left({\frac {\lambda }{2\pi }}\right)^{\frac {n}{2}}\left(\prod _{i=1}^{n}{\frac {w_{i}}{X_{i}^{3}}}\right)^{\frac {1}{2}}\exp \left({\frac {\lambda }{\mu }}\sum _{i=1}^{n}w_{i}-{\frac {\lambda }{2\mu ^{2}}}\sum _{i=1}^{n}w_{i}X_{i}-{\frac {\lambda }{2}}\sum _{i=1}^{n}w_{i}{\frac {1}{X_{i}}}\right).$

En résolvant l'équation de vraisemblance, on obtient les estimées suivantes :

${\hat {\mu }}={\frac {\sum _{i=1}^{n}w_{i}X_{i}}{\sum _{i=1}^{n}w_{i}}},\,\,\,\,\,\,\,\,{\frac {1}{\hat {\lambda }}}={\frac {1}{n}}\sum _{i=1}^{n}w_{i}\left({\frac {1}{X_{i}}}-{\frac {1}{\hat {\mu }}}\right).$

${\hat {\mu }}$ et ${\hat {\lambda }}$ sont indépendants et

${\hat {\mu }}\sim IG\left(\mu ,\lambda \sum _{i=1}^{n}w_{i}\right)\,\,\,\,,\,\,\,\,{\frac {n}{\hat {\lambda }}}\sim {\frac {1}{\lambda }}\chi _{n-1}^{2}.$

Simulation numérique de la loi inverse-gaussienne

L'algorithme suivant peut être utilisé pour générer des valeurs de la loi inverse-gaussienne.

Prendre $N\sim {\mathcal {N}}(0,1)$

et $y=N^{2}$

et $X=\mu +{\frac {\mu ^{2}y}{2\lambda }}-{\frac {\mu }{2\lambda }}{\sqrt {4\mu \lambda y+\mu ^{2}y^{2}}}$.

Prendre $Z\sim {\mathcal {U}}(0,1).$

Si $Z\leq {\frac {\mu }{\mu +x}}$retourner $x$

Sinon retourner ${\frac {\mu ^{2}}{x}}$

Liens avec d'autres lois

La convolution de la loi inverse-gaussienne et de la loi exponentielle est utilisée comme modélisation du temps de réponse en psychologie. Elle est appelée loi ex-Wald.

Historique

Cette loi fut initialement utilisée par Erwin Schrödinger en 1915 comme temps d'atteinte du mouvement brownien. Le nom « inverse-gaussienne » (inverse Gaussian en anglais) fut proposé par Tweedie en 1945. Abraham Wald réutilise cette loi en 1947 comme la forme limite d'un échantillon dans un test. Tweedie détaille des propriétés statistiques de cette loi en 1957.

Logiciel

Le langage de programmation R possède cette loi.

Notes et références

Références

• The inverse gaussian distribution: theory, methodology, and applications by Raj Chhikara and Leroy Folks, 1989 (ISBN 0-8247-7997-5)
• System Reliability Theory by Marvin Rausand and Arnljot Høyland
• The Inverse Gaussian Distribution by Dr. V. Seshadri, Oxford Univ Press, 1993