Épigraphe (mathématiques)

Soit $f$ une fonction définie sur un ensemble $\mathbb {E}$ à valeurs dans la droite réelle achevée ${\overline {\mathbb {R} }}=\mathbb {R} \cup \{-\infty ,+\infty \}$. L'épigraphe de $f$ est l'ensemble noté $\operatorname {epi} \,f$ et défini par

Représentation d'une portion de l’épigraphe d'une fonction f(x) (en vert).

$\operatorname {epi} \,f:=\{(x,\alpha )\in \mathbb {E} \times \mathbb {R} :f(x)\leqslant \alpha \}.$

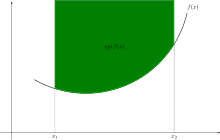
Il s'agit donc de l'ensemble des points de l'ensemble produit $\mathbb {E} \times \mathbb {R}$ qui sont situés au-dessus du graphe de $f$ (épi venant du grec ancien et signifiant sur, au-dessus).

L'épigraphe strict de $f$ est l'ensemble noté $\operatorname {epi} _{s}\,f$ et défini par

$\operatorname {epi} _{s}\,f:=\{(x,\alpha )\in \mathbb {E} \times \mathbb {R} :f(x)<\alpha \}.$

Exemples d'utilisation

L'épigraphe permet de transférer aux fonctions des notions définies pour les ensembles. En voici deux exemples.

• Si $\mathbb {E}$ est un espace topologique, on démontre qu'une application $f:\mathbb {E} \to {\overline {\mathbb {R} }}$ est semi-continue inférieurement si et seulement si son épigraphe est un fermé de l'espace topologique produit $\mathbb {E} \times \mathbb {R}$. En analyse convexe, une telle application est dite fermée.
• Si $\mathbb {E}$ est un espace vectoriel réel, on dit que $f:\mathbb {E} \to {\overline {\mathbb {R} }}$ est convexe si son épigraphe est un convexe de l'espace vectoriel produit $\mathbb {E} \times \mathbb {R}$.

Article connexe

Hypographe