Théorème de Morley

En mathématiques, et plus précisément en géométrie plane, le théorème de Morley, découvert par Frank Morley en 1898, affirme que les intersections des trissectrices des angles d'un triangle forment un triangle équilatéral.

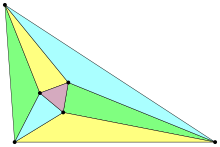
Le triangle équilatéral ainsi défini par le théorème de Morley s'appelle le « triangle de Morley » du triangle de départ.

Démonstrations

Il existe de nombreuses démonstrations de ce théorème. Ci-dessous sont présentées trois démonstrations : une n'utilisant que des propriétés de géométrie élémentaire, les deux autres travaillant sur la trigonométrie ou les complexes offrant l'avantage de fournir la dimension du triangle équilatéral.

Démonstration en géométrie élémentaire

Triangle de Morley et son « tripode ».

Claude Frasnay propose une démonstration sans trigonométrie ni nombres complexes, utilisant uniquement la somme des angles d'un triangle et les similitudes directes.

Pour tous réels strictement positifs $a,b,c$ tels que $a+b+c={\frac {\pi }{3}},$ est appelé « dipode de pointure $(a,b),$ » la figure $\mathrm {QARBP}$ constituée d'un triangle équilatéral direct $\mathrm {QRP}$ auquel on adjoint deux triangles de sens direct $\mathrm {QAR}$ et $\mathrm {RBP}$ tels que les angles de sommets $\mathrm {A}$ et $\mathrm {B}$ aient pour mesure en radians a et b et les angles de sommets $\mathrm {Q}$ et $\mathrm {P}$ aient pour mesure ${\frac {\pi }{3}}+c.$ Par construction, deux dipodes de même pointure sont directement semblables.

De même est appelé « tripode de pointure $(a,b,c)$ », la figure $\mathrm {QRPABC}$ constituée de trois dipodes $\mathrm {QARBP}$ de pointure $(a,b),$ $\mathrm {RBPCQ}$ de pointure $(b,c)$ et $\mathrm {PCQAR}$ de pointure $(c,a).$ Par construction, deux tripodes de même pointure sont directement semblables.

Pour un tripode $\mathrm {QRPABC}$ donné de pointure $(a,b,c),$ on construit ensuite le triangle $\mathrm {ABW'}$ direct tel que les angles de sommet $\mathrm {A}$ et $\mathrm {B}$ mesurent $2a$ et $2b.$ On appelle $\mathrm {R'}$ le point de concours des bissectrices de ce triangle et on construit un triangle équilatéral direct $\mathrm {Q'R'P'}$ symétrique par rapport à $\mathrm {R'W'}$ et tel que $\mathrm {P'}$ et $\mathrm {Q'}$ appartiennent respectivement à $[\mathrm {BW'} ]$ et $[\mathrm {AW'} ]$. On démontre alors que $\mathrm {Q'AR'BP'}$ est un bipode de pointure $(a,b).$ Comme deux bipodes de même pointure sont directement semblables, les bipodes $\mathrm {QARBP}$ et $\mathrm {Q'AR'BP'}$ sont semblables et confondus, et les demi-droites $[\mathrm {AR} )$ et $[\mathrm {BR} )$ sont les bissectrices intérieures des angles $\mathrm {QAB}$ et $\mathrm {ABP.}$ En reprenant le même raisonnement sur $[\mathrm {BC} ]$ puis $[\mathrm {CA} ]$, on démontre que les demi-droites $[\mathrm {AQ} )$, $[\mathrm {AR} )$, $[\mathrm {BR} )$, $[\mathrm {BP} )$, $[\mathrm {CP} )$ et $[\mathrm {CQ} )$ sont les trisectrices du triangle $\mathrm {ABC}$ dont les angles aux sommets sont donc $3a,\,3b,\,3c.$

Tout triangle $\mathrm {A'B'C'}$ direct d'angles $3a,\,3b,\,3c$ est directement semblable au triangle $\mathrm {ABC}$ construit à partir du tripode de pointure $(a,b,c)$ et ses trisectrices se coupent donc en formant un triangle équilatéral directement semblable au triangle $\mathrm {QRP}$.

Démonstration à l'aide de la trigonométrie

La loi des sinus détermine la longueur de la plupart des segments à partir des côtés du triangle et le théorème d'Al-Kashi permet de déterminer les autres, notamment les trois côtés PR, PQ et QR du triangle rouge — celui qui est censé être équilatéral.

On définit les angles $a$, $b$ et $c$ tels que :

• ${\widehat {\mathrm {BAC} }}=3\times a,$
• ${\widehat {\mathrm {CBA} }}=3\times b,$
• ${\widehat {\mathrm {ACB} }}=3\times c.$

Puisque dans tout triangle on a :

${\widehat {\mathrm {BAC} }}+{\widehat {\mathrm {CBA} }}+{\widehat {\mathrm {ACB} }}=\pi ,$

le changement de variable ci-dessus donne :

$a+b+c={\frac {\pi }{3}}.$

De plus, pour simplifier les calculs, on adopte une unité de longueur telle que le rayon du cercle circonscrit au triangle est 1. On a alors :

• AB = 2 sin(3c),
• BC = 2 sin(3a),
• AC = 2 sin(3b).

Dans le triangle BPC, d'après la loi des sinus, on a :

${\frac {\mathrm {BP} }{\sin(c)}}={\frac {\mathrm {BC} }{\sin(\pi -b-c)}}={\frac {2\sin(3a)}{\sin(b+c)}}={\frac {2\sin(3a)}{\sin({\frac {\pi }{3}}-a)}}$

$\mathrm {BP} ={\frac {2\sin(3a)\sin(c)}{\sin({\frac {\pi }{3}}-a)}}.$

On peut développer sin(3a) :

${\begin{aligned}\sin(3a)&=(3-4\sin ^{2}a)\sin a\\&=(3\cos ^{2}a-\sin ^{2}a)\sin a\\&=4\left({\tfrac {\sqrt {3}}{2}}\cos a+{\tfrac {1}{2}}\sin a\right)\left({\tfrac {\sqrt {3}}{2}}\cos a-{\tfrac {1}{2}}\sin a\right)\sin a\\&=4\sin \left({\tfrac {\pi }{3}}+a\right)\sin \left({\tfrac {\pi }{3}}-a\right)\sin a,\end{aligned}}$

ce qui permet de simplifier l'expression de BP :

$\mathrm {BP} =8\sin(a)\sin(c)\sin \left({\tfrac {\pi }{3}}+a\right).$

On obtiendrait de même :

$\mathrm {BR} =8\sin(a)\sin(c)\sin \left({\tfrac {\pi }{3}}+c\right).$

En appliquant alors le théorème d'Al-Kashi, qui s'écrit PR² = BP² + BR² – 2 BP BR cos(b), on obtient :

$\mathrm {PR} ^{2}=64\sin ^{2}(a)\sin ^{2}(c)\left[\sin ^{2}\left({\tfrac {\pi }{3}}+a\right)+\sin ^{2}\left({\tfrac {\pi }{3}}+c\right)-2\sin \left({\tfrac {\pi }{3}}+a\right)\sin \left({\tfrac {\pi }{3}}+c\right)\cos(b)\right].$

Or

$\left({\tfrac {\pi }{3}}+a\right)+\left({\tfrac {\pi }{3}}+c\right)+b={\tfrac {2\pi }{3}}+(a+b+c)=\pi .$

Il existe donc un triangle ayant pour angles ${\tfrac {\pi }{3}}+a,\;{\tfrac {\pi }{3}}+c,{\text{ et }}b,$ et dont le rayon du cercle circonscrit est 1. Si on lui applique le théorème d'Al-Kashi, on a :

$\sin ^{2}(b)=\sin ^{2}\left({\tfrac {\pi }{3}}+a\right)+\sin ^{2}\left({\tfrac {\pi }{3}}+c\right)-2\sin \left({\tfrac {\pi }{3}}+a\right)\sin \left({\tfrac {\pi }{3}}+c\right)\cos(b)$

donc

$\mathrm {PR} =8\sin(a)\sin(c)\sin(b).$

On obtiendrait de même

$\mathrm {PQ} =8\sin(a)\sin(b)\sin(c){\text{ et }}\mathrm {QR} =8\sin(b)\sin(c)\sin(a),$

ce qui prouve que PR = PQ = QR. Le triangle PQR est donc bien équilatéral.

Démonstration à l'aide des complexes

Cette démonstration est basée sur un article d'Alain Connes. Elle utilise les nombres complexes et donne un calcul rapide de l'affixe des sommets du triangle équilatéral.

On se place dans le plan euclidien orienté qu'on pourra ultérieurement identifier au corps des complexes. On désigne par P, Q et R les trois intersections de trisectrices dont on veut montrer qu'elles forment un triangle équilatéral. En outre, on place les points P', Q' et R' symétriques de P, Q et R respectivement par rapport à BC, CA, 'AB (voir figure ci-contre). On note enfin comme précédemment $3a,\;3b,\;3c$ les angles ${\widehat {\mathrm {BAC} }},\;{\widehat {\mathrm {CBA} }},\;{\widehat {\mathrm {ACB} }}$.

Soient maintenant f, g, h les rotations de centres respectifs A, B, C et d'angles respectifs $2a,\;2b,\;2c$. On observe alors que :

• (i) P (resp. Q, R) est le point fixe de $g\circ h$ (car il est centre de cette rotation) (resp. ${h\circ f,\;f\circ g}$ ).

  En effet h transforme P en P' et g transforme P' en P. Il en est de même pour Q et R.

• (ii) $f^{3}\circ g^{3}\circ h^{3}=I$ (application identité).

  En effet la somme des angles des rotations composantes est 2π et on obtient donc une translation. Mais A est invariant puisque h³ (rotation de centre C et d'angle $2{\widehat {\mathrm {ACB} }}$) transforme A en A' symétrique de A par rapport à BC, g³ transforme A' en A et finalement f³ laisse A invariant. Par suite cette translation est l'application identité.

Ainsi, on peut désormais travailler dans le corps des complexes en conservant les notations que nous avons introduites. On définit simplement les rotations f, g, h par

$f(z)=a_{1}z+b_{1}$

$g(z)=a_{2}z+b_{2}$

$h(z)=a_{3}z+b_{3}$

avec $a_{1},a_{2},a_{3}$ égaux respectivement à ${\rm {e}}^{2{\rm {i}}a},{\rm {e}}^{2{\rm {i}}b},{\rm {e}}^{2{\rm {i}}c}$.

Un calcul rapide montre que (i) équivaut à

$\mathrm {P} ={\frac {a_{2}b_{3}+b_{2}}{1-a_{2}a_{3}}}$

$\mathrm {Q} ={\frac {a_{3}b_{1}+b_{3}}{1-a_{3}a_{1}}}$

$\mathrm {R} ={\frac {a_{1}b_{2}+b_{1}}{1-a_{1}a_{2}}}.$

Quant à (ii) on montre l'équivalence avec

• (iii) 
  • $(a_{1}a_{2}a_{3})^{3}=1$ ;
  • $(a_{1}^{2}+a_{1}+1)b_{1}+a_{1}^{3}(a_{2}^{2}+a_{2}+1)b_{2}+(a_{1}a_{2})^{3}(a_{3}^{2}+a_{3}+1)b_{3}=0$.

Le complexe $\mathrm {j} :=a_{1}a_{2}a_{3}$ est différent de 1 donc est l'une des deux racines cubiques primitives de l'unité. On a alors

$\mathrm {P} ={\frac {a_{1}(a_{2}b_{3}+b_{2})}{a_{1}-\mathrm {j} }}$

$\mathrm {Q} ={\frac {a_{2}(a_{3}b_{1}+b_{3})}{a_{2}-\mathrm {j} }}$

$\mathrm {R} ={\frac {a_{3}(a_{1}b_{2}+b_{1})}{a_{3}-\mathrm {j} }}.$

Ces trois égalités sont bien définies car le triangle n'est pas plat, donc aucun des angles $3a,3b,3c$ ne vaut ±π.

On peut alors vérifier que $\mathrm {R} +j\mathrm {P} +j^{2}\mathrm {Q} =0$, ce qui est une caractérisation classique du caractère équilatéral du triangle PQR.

Démonstration de $\mathrm {R} +j\mathrm {P} +j^{2}\mathrm {Q} =0$

On développe $(\mathrm {R} +j\mathrm {P} +j^{2}\mathrm {Q} )(a_{1}-\mathrm {j} )(a_{2}-\mathrm {j} )(a_{3}-\mathrm {j} )$, en utilisant que le complexe $\mathrm {j} :=a_{1}a_{2}a_{3}$ vérifie $1+\mathrm {j} +\mathrm {j} ^{2}=0.$

Le coefficient de b₁ dans l'expression ci-dessus est

$a_{3}(a_{1}-\mathrm {j} )[a_{2}-\mathrm {j} +\mathrm {j} ^{2}a_{2}(a_{3}-\mathrm {j} )]=a_{3}(a_{1}-\mathrm {j} )(-\mathrm {j} +1/a_{1})=-{\frac {\mathrm {j} a_{3}}{a_{1}}}(a_{1}^{2}+a_{1}+1)$.

Le coefficient de b₂ est

$a_{1}(a_{2}-\mathrm {j} )[a_{3}(a_{1}-\mathrm {j} )+\mathrm {j} (a_{3}-\mathrm {j} )]=\mathrm {j} a_{1}(a_{2}-\mathrm {j} )(-\mathrm {j} +1/a_{2})=-{\frac {\mathrm {j} ^{2}a_{1}}{a_{2}}}(a_{2}^{2}+a_{2}+1)$.

Enfin, le coefficient de b₃ est

$a_{2}(a_{3}-\mathrm {j} )[\mathrm {j} a_{1}(a_{2}-\mathrm {j} )+\mathrm {j} ^{2}(a_{1}-\mathrm {j} )]=\mathrm {j} ^{2}a_{2}(a_{3}-\mathrm {j} )(-\mathrm {j} +1/a_{3})=-{\frac {a_{2}}{a_{3}}}(a_{3}^{2}+a_{3}+1)$.

Finalement,

${\begin{aligned}(R+j\mathrm {P} +j^{2}\mathrm {Q} )(a_{1}-j)(a_{2}-j)(a_{3}-j)&\\=&-{\frac {1}{ja_{1}^{2}a_{2}}}[(a_{1}^{2}+a_{1}+1)b_{1}+a_{1}^{3}(a_{2}^{2}+a_{2}+1)b_{2}+(a_{1}a_{2})^{3}(a_{3}^{2}+a_{3}+1)b_{3}]=0\quad {\text{ (cf. (iii))}}\end{aligned}}$.

Autres propriétés du triangle de Morley

Longueur des côtés

Chaque côté du triangle de Morley mesure :

$8R\sin {\frac {\widehat {A}}{3}}\sin {\frac {\widehat {B}}{3}}\sin {\frac {\widehat {C}}{3}},$

où ${\widehat {A}},{\widehat {B}},{\widehat {C}}$ désignent les angles en A,B,C du triangle et où $R$ désigne le rayon du cercle circonscrit.

Orientation du triangle de Morley

• Orientation par rapport au triangle de départ : le côté $(B'C')$ du triangle de Morley situé le plus près du sommet A fait avec le côté $(BC)$ du triangle de départ un angle égal à ${{\widehat {C}}-{\widehat {B}}} \over 3$.
• Orientation par rapport à la deltoïde de Steiner : le triangle (équilatéral) formé par les points de rebroussement de la deltoïde de Steiner et le triangle (équilatéral) de Morley, ont leurs côtés parallèles.

Centres de Morley

On appelle centres de Morley deux centres du triangle points de Morley. Ils portent les nombres de Kimberling X₃₅₆ (premier centre de Morley, le centre de gravité du triangle de Morley) et X₃₅₇ (deuxième centre de Morley, premier centre de Morley–Taylor–Marr, ou point de concours des droites AP, BQ, CR).

Coordonnées trilinéaires

Les coordonnées trilinéaires du premier centre de Morley sont

$\cos(A/3)+2\cos(B/3)\cos(C/3):\cos(B/3)+2\cos(C/3)\cos(A/3):\cos(C/3)+2\cos(A/3)\cos(B/3).$

Les coordonnées trilinéaires du deuxième centre de Morley sont

$\sec(A/3):\sec(B/3):\sec(C/3).$

Historique

Après la découverte de ce théorème par Frank Morley à la fin du XIX^e siècle, les collègues de ce dernier trouvaient le résultat si beau qu'ils lui ont donné le nom de « miracle de Morley ». Comme l'écrit Richard Francis : « Apparemment ignoré par les géomètres antérieurs ou hâtivement abandonné en raison d'incertitudes liées à la trisection et à la constructibilité, le problème n'apparut réellement qu'il y a un siècle. » Par ailleurs, même si Morley a proposé une solution au problème, la preuve rigoureuse du théorème a été plus tardive.

Lien externe

• Théorème de Morley sur le site abracadabri (associé à Cabri Géomètre) ; on y verra décrits 18 triangles équilatéraux avec des sommets sur des trisectrices généralisées issues des 3 sommets du triangle et 36 triangles avec des sommets sur des trisectrices issues de 2 sommets du triangle.
• (en) [vidéo] Mathologer, Math is Illuminati confirmed (PART 2): Morley's Miracle sur YouTube, une preuve géométrique animée du théorème de Morley, due à John Conway.