Puissance résiduelle

La puissance résiduelle d'un réacteur nucléaire est la chaleur produite par le cœur postérieurement à l'arrêt de la réaction nucléaire en chaîne et constituée par l'énergie de désintégration des produits de fission.

Puissance résiduelle après arrêt instantané du réacteur.

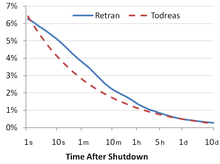
Dans le cas d'un réacteur électrogène ayant fonctionné un an à sa pleine puissance et brusquement arrêté, la puissance résiduelle instantanée vaut 6,5 % de la puissance thermique du réacteur immédiatement avant son arrêt ; elle décroît ensuite et vaut typiquement par valeur supérieure : 2,67 % quinze minutes après l'arrêt, 1,59 % après une heure, 0,67 % après une journée et 0,34 % après une semaine. L'énergie totale de désintégration des produits de fission représente un peu moins de 40 %, de l'énergie d'une journée de fonctionnement du réacteur à pleine puissance. Cette énergie est libérée pour l'essentiel dans les trois ans suivant l'arrêt du réacteur.

Cette chaleur n'est pas matériellement réductible, elle doit impérativement être évacuée, même en cas d'indisponibilité des moyens normaux d'extraction de puissance du cœur, faute de quoi elle peut mener à la fusion du cœur. Ce phénomène est d'une importance majeure pour la conception des systèmes de sécurité du réacteur : la puissance résiduelle est responsable de la ruine des réacteurs de Three Miles Island et de Fukushima.

Pour autant, la puissance électrique nécessaire à l'extraction de la chaleur (par évaporation d'eau à 15 °C) à l'aide d'une pompe reste modérée.

Présentation

Dans un réacteur nucléaire, la chaleur récupérable produite par les fissions se décompose comme indiqué à l'article fission nucléaire :

Composante de l'énergie de fission	Part d'énergie récupérable (%)	Commentaire
Énergie cinétique des fragments de fission	85,9	énergie instantanée localisée
Énergie cinétique des neutrons de fission	2,8	énergie instantanée délocalisée
Énergie des rayons gamma (γ) de fission	3,9	énergie instantanée délocalisée
Énergie de radioactivité β des produits de fission	3,7	énergie différée
Énergie de radioactivité γ des produits de fission	3,7	énergie différée
Énergie récupérable en réacteur de puissance	100,0

Au cours du fonctionnement du réacteur, la puissance thermique totale ci-dessus est extraite du cœur ou des structures proches de celui-ci, mais en cas d'arrêt du réacteur, la chaleur dégagée par les produits de fissions en cours de désintégration continue d'être produite jusqu'à atteindre un état stable.

On appelle cette chaleur puissance résiduelle du réacteur. On donne sa valeur dans le tableau ci-dessous dans un cas enveloppe type (voir section sur l'histogramme enveloppe). Dans ce tableau, la puissance et l'énergie résiduelle sont évaluées à l'aide du modèle à dix groupes de radionucléides présenté en fin d'article.

On peut noter dans ce tableau que, avec un réseau d'hypothèses pénalisantes, la puissance électrique nécessaire à l'évacuation de la puissance résiduelle d'un réacteur à eau pressurisée (REP) de type N4 de 1 450 MWe une heure après l'arrêt, au moyen d'une pompe d'injection fournissant un débit d'eau à température ordinaire destiné à être évaporé, ne dépasse pas 300 kWe.

Puissance et énergie résiduelles d'un réacteur électrogène de 4 250 MWth après un an de fonctionnement continu à pleine puissance

Temps t depuis l'arrêt	Puissance résiduelle par valeur supérieure (%)	Puissance résiduelle par valeur supérieure (MW)	Délai équivalent d'échauffement à 100 °C de 2 500 m3 d'eau initialement à 15 °C, avec la puissance résiduelle à t	Énergie produite (JEPN)	Quantité équivalente d'eau évaporée (initialement à 15 °C) avec l'énergie produite (tonne)	Débit correspondant (kg/s)	Puissance électrique de la pompe refoulant le débit à 50 bar (kW)	Commentaire
1 s	7,54 %	320	40 min	9,25E-7	0,130	123,1	1 231	Cas théorique
10 s	5,83 %	247	53 min	7,54E-6	1,06	95,3	953	Cas théorique
1 min	4,5 %	191	1,1 h	3,62E-5	5,11	73,4	734	Instant d'étouffement des fissions retardées
10 min	3,0 %	127,3	1,7 h	2,55E-4	36,4	48,9	489
30 min	2,1 %	88,5	2,5 h	5,97E-4	85,3	34,0	340	Cas d'arrêt normal
1 h	1,59 %	67,6	3,2 h	9,71E-4	137	26,0	260	Cas d'arrêt normal
2 h	1,34 %	57,1	3,8 h	1,57E-3	221	21,9	219
5 h	1,13 %	47,9	4,6 h	3,10E-3	437	18,4	184
12 h	0,855 %	36,4	6,0 h	5,94E-3	838	14,0	140
1 j	0,67 %	28,6	7,6 h	9,68E-3	1 365	11,0	110
3 j	0,49 %	20,7	10,5 h	0,0209	2 950	7,97	79,7
1 sem.	0,34 %	14,5	15,0 h	0,0371	5 230	5,59	55,9	Renouvellement du combustible
1 mois (30,44 j)	0,167 %	7,09	31 h	0,0893	12 700	2,72	27,2	Assemblages usagés en piscine
3 mois (91,31 j)	0,088 %	3,74	58 h	0,161	22 760	1,44	14,4	Assemblages usagés en piscine
6 mois (182,62 j)	0,048 %	2,06	4,4 j	0,221	31 230	0,79	7,9
1 an	0,018 %	0,784	11,6 j	0,277	39 040	0,301	3,0	Séjour à long terme en piscine

Conception des réacteurs - histogramme de puissance enveloppe

Pour définir les moyens d'extraction de puissance résiduelle, on définit un ou plusieurs histogrammes types de fonctionnement du réacteur qui déterminent la puissance résiduelle à évacuer post-arrêt. Dans le cas d'un réacteur électrogène censé fonctionner en base, on retient généralement un an de fonctionnement continu à pleine puissance pour les évaluations de sûreté, on tient compte du délai d'arrêt de la tranche et de refroidissement pour évaluer la puissance résiduelle du combustible en vue de son renouvellement. Les rythmes d'exploitation des réacteurs expérimentaux et de propulsion navale sont différents.

Dès lors qu'un histogramme maximal d'emploi du réacteur a été défini comme servant de base au dimensionnement des moyens de sécurité, le réacteur devra ultérieurement rester à l'intérieur de ce domaine d'emploi dans le cours de son utilisation, sauf à établir que l'usage fait du réacteur ne conduit pas à dépasser la puissance prise en compte dans le dimensionnement des moyens de sécurité.

De façon à éviter des calculs longs et fastidieux et à prendre des marges de dimensionnement, la démarche consiste à définir un histogramme enveloppe d'emploi du réacteur, en effectuer le calcul précis à l'aide d'un outil de calcul complet, et à majorer ensuite le résultat précis non aisément manipulable avec des corrélations simplifiées.

Conception des réacteurs - Corrélations de puissance résiduelle

D'une façon générale, la modélisation de la puissance résiduelle et restée relativement imprécise jusqu'au milieu des années 1980 en raison de la lourdeur du calcul et de sa faible importance au regard d'autres priorités.

Corrélations de la littérature technique

Évolution de la puissance résiduelle suivant différentes corrélations^{[Lesquelles ?]} ― échelle linéaire.

Plusieurs corrélations ont été proposées pour évaluer la puissance résiduelle, dont les plus classiques sont présentées ci-après.

• Notations utilisées :

  Wr = puissance résiduelle

  Po = puissance du réacteur avant l'arrêt

  d = durée de fonctionnement du réacteur

  t = temps écoulé depuis l'arrêt du réacteur

  Origine des temps = Instant d'arrêt du réacteur

• Les modèles supposent un fonctionnement à puissance constante ; si le réacteur a effectué plusieurs paliers de puissance, il convient d’additionner les contributions de chaque palier.
• Une première formule approchée a été élaborée par Way et Wigner en 1946

${Wr(t) \over P_{o}}=0,0622*(t^{-0,2}-(d+t)^{-0,2})$ avec $t$ et $d$ en secondes applicable entre 10 s et 100 jours post arrêt

• Corrélation de Todreas Kazimi (reprise / correction de la corrélation de Way - Wigner par augmentation de 6 % du coefficient en facteur) :

${Wr(t) \over P_{o}}=0,066*(t^{-0,2}-(d+t)^{-0,2})$ avec $t$ et $d$ en secondes applicable entre 10 s et 100 jours post arrêt

• Corrélation de Todreas Rust

${Wr(t) \over P_{o}}=0,1*\left[(t+10)^{-0,2}-(t+d+10)^{-0,2}-0,87*\left((t+2E7)^{-0,2}-(t+d+2E7)^{-0,2}\right)\right]$ avec $t$ et $d$ en secondes applicable entre 1 s et 10 jours post arrêt

Évolution de la puissance résiduelle suivant différentes corrélations^{[Lesquelles ?]} ― échelle logarithmique.

• Corrélation générale

${Wr(t) \over P_{o}}=a*(t^{-b}-(d+t)^{-b})$ de t = 0,1 à 10 s, a = 0,06025 b = 0,6390 de t = 10 à 150 s, a = 0,07655 b = 0,1807 de t = 150 à 8E8 s, a = 0,13715 b = 0,2962 applicable entre 0,1 s et 1 an post-arrêt

Justification des corrélations en$.\;t^{-0,2}\;.$

Les corrélations en$.\;t^{-0,2}\;.$trouvent une justification dans la règle semi-empirique de Sargent, du nom du physicien canadien Bernice Weldon Sargent (en) qui énonça dans les années 1930 la règle suivant laquelle la vie moyenne d'un émetteur bêta est inversement proportionnelle à la puissance 5 de l'écart d'énergie de cohésion entre l'atome père et l'atome fils : $.\quad \lambda \div \delta E^{5}\quad .$ Suivant cette règle, on peut admettre que la chaleur dégagée à l'instant t après arrêt du réacteur par les produits de fission de vie moyenne égale à t formés à l'instant (o) d'arrêt du réacteur, est proportionnelle à $.\;t^{-1}*t^{-0,2}\;.$ ;avec $.\;t^{-1};.$ proportionnel à la quantité et $.\;t^{-0,2}\;.$ proportionnel à l'énergie. De la même façon, la chaleur des produits de fission de vie moyenne égale à t - u, formés au cours du palier de puissance dans l'intervalle de temps u ; u + du est proportionnelle à $.\quad dWr\div (t-u)^{-1,2}\quad .$ (u est négatif). On fait alors l'hypothèse que dans l'ensemble des produits de fission, les vies moyennes sont équiprobables d'où

$.\quad Wr(t)\div \int \limits _{-d}^{0}(t-u)^{-1,2}*du\div \left(t^{-0,2}-(t+d)^{-0,2}\right)\quad .$

Le coefficient de proportionnalité (voisin de 0,066) découle assez simplement de la valeur de l'énergie en bêta et gamma différés dans la décomposition de l'énergie de fission récupérable en réacteur, soit 7,4 % environ, en tenant compte de ce que les formules en t^-0,2 ne sont de toutes façons pas calculables au voisinage de t = 0.

Il est par ailleurs assez remarquable qu'une approche aussi simpliste conduise à un résultat aussi voisin de la réalité constatée.

Exemple de modélisation plus complète

Un calcul plus complet consiste à modéliser la puissance produite par les produits de fissions comme la somme de celles de groupes de corps de périodes régulièrement étagées. À chaque groupe est associé une contribution à la puissance dégagée qui rend compte du nombre d'atomes désintégrés et de l'énergie correspondante. Par exemple un regroupement en dix groupes est souvent utilisé et donne d'assez bons résultats. Dans ce calcul simplifié l'effet des neutrons retardés et des actinides peut être pris en compte, les contributions respectives à la puissance thermique totale sont confondues avec celles des groupes 1, 2 et 10 respectivement.

Le modèle consiste ; en un premier temps à évaluer la contribution à la puissance instantanée de chacun des groupes à l'instant d'arrêt du réacteur compte tenu de l'histogramme de puissance antérieur ; en un second temps à évaluer la puissance de chacun des groupes postérieurement à l'arrêt du réacteur. L'origine des temps est placée à l'instant d'arrêt.

• On raisonne tout d'abord dans le cas où il n'y aurait qu'un seul groupe de radionucléides et un seul palier de puissance.
  La quantité de radionucléides dQ produite durant l'intervalle de temps dt dans le cours du palier est proportionnelle à la puissance et égale à $.\qquad dQ=\alpha *P*dt\qquad .$À l'issue du palier, cette quantité dQ devient $dQ*e^{\lambda *t}\qquad .$ (l'origine des temps étant à la fin du palier, t est négatif). La quantité de radionucléides à l'issue d'un palier de durée d, effectué à la puissance P constante est égale à

$Q(o)=\int _{-d}^{o}dQ*e^{\lambda *t}=\int _{-d}^{o}\alpha *P*e^{\lambda *t}*dt={\alpha \over \lambda }*P*(1-e^{-\lambda *d})$

Si e est l'énergie de désintégration, la puissance résiduelle émise par la quantité Q de radionucléides présents à la fin du palier est égale à $.\qquad Wr(o)=\lambda *Q*e=e*\alpha *P*(1-e^{-\lambda *d})\qquad .$. A l'instant t post arrêt du réacteur la puissance résiduelle vaut :

$Wr(t)=Wr(o)*e^{-\lambda *t}=e*\alpha *P*(1-e^{-\lambda *d})*e^{-\lambda *t}\qquad .$

L'énergie dégagée à l'instant t après arrêt du réacteur (E(t)) prend la valeur simple

$E(t)=Wr(o)*(1-e^{-\lambda *t})$

• S'il y a plusieurs paliers de puissance successifs, la formule est aisément généralisable par simple sommation. Par exemple dans un histogramme à trois paliers de puissance P1, P2, P3 et de durées respectives d1, d2,d3 on additionne les contributions respectives de chacun des paliers à l'instant d'arrêt du réacteur en tenant compte de la décroissance des radionucléides produit durant le premier palier au cours des deux derniers paliers et ainsi de suite ; on aura donc :

$Q(o)=Q1(o)+Q2(o)+Q3(o)=\alpha *[P1*(1-e^{-\lambda *d1})*e^{-\lambda *(d2+d3)}+P2*(1-e^{-\lambda *d2})*e^{-\lambda *d3}+P3*(1-e^{-\lambda *d3})]$

$Wr(o)=e*Q(o)=e*\alpha *[P1*(1-e^{-\lambda *d1})*e^{-\lambda *(d2+d3)}+P2*(1-e^{-\lambda *d2})*e^{-\lambda *d3}+P3*(1-e^{-\lambda *d3})]$

$Wr(t)=e*\alpha *[P1*(1-e^{-\lambda *d1})*e^{-\lambda *(d2+d3)}+P2*(1-e^{-\lambda *d2})*e^{-\lambda *d3}+P3*(1-e^{-\lambda *d3})]*e^{-\lambda *t}$

• On tient compte maintenant des 10 groupes de radionucléides par sommation de la contribution de chaque groupe.

$Wr(t)=\sum _{i=1}^{10}Wri(t)$

Les valeurs des termes (ei × αi) de i = 1 jusqu'à 10 sont données dans le tableau ci-après dans un cas typique. L'évaluation correspondante est correcte, cependant dans le cas d'un calcul de sûreté il convient de majorer le résultat de façon forfaitaire en multipliant par 1,246. Ce coefficient est le produit de trois facteurs^{[réf. nécessaire]} :

• une incertitude générale sur la puissance thermique estimée à 1,03 ;
• un écart entre le résultat du calcul complet et la réalité estimé à 1,1 ;
• un écart de calcul entre le modèle complet et le calcul simplifié (comparaison « code à code » estimée à 1,1).

En résulte le coefficient global de majoration du résultat, égal à 1,246, qui permet d’assurer que le résultat du calcul est bien supérieur à la puissance thermique résiduelle à tous les instants post arrêt du réacteur

• L'énergie dégagée post-arrêt E(t) est également aisément calculable par sommation

$E(t)=\sum _{i=1}^{10}{Wri(o) \over \lambda _{i}}*(1-e^{-\lambda _{i}*d3})*e^{-\lambda _{i}*t}$

$E(\infty )=\sum _{i=1}^{10}{Wri(o) \over \lambda _{i}}$

Exemple de groupage des produits de fission par période radioactive

Groupe	Période (s)	Constante radioactive (s−1)	Vie moyenne (s-min-h-j)	Contribution = ei × αi (%)	Commentaire
1	1	6,93147E-1	1,4 s	1,420 %	Comprend la contribution des fissions générées par les neutrons retardés
2	10	6,93147E-2	14,4 s	1,260 %	Comprend la contribution des fissions générées par les neutrons retardés
3	50	1,38629E-2	72,1 s	0,755 %
4	200	3,46574E-3	4,8 min	0,470 %
5	1 000	6,93147E-4	24,0 min	1,740 %
6	20 000	3,46574E-5	8,0 h	0,615 %
7	200 000	3,46574E-6	80,1 h	0,290 %
8	1 000 000	6,93147E-7	16,7 j	0,174 %
9	8 000 000	8,66434E-8	133,6 j	0,130 %
10	80 000 000	8,66434E-9	1336 j	0,038 %	Comprend la contribution des actinides
Total	Sans signification			6,892 %	L'équilibre des groupes 9 et 10 n'est pas atteint au bout d'un an de fonctionnement

Références

• (de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Nachzerfallswärme » (voir la liste des auteurs).

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Decay heat » (voir la liste des auteurs).