Magnéton de Bohr

En physique atomique, le magnéton de Bohr-Procopiu ou magnéton de Bohr (électronique) (symbole $\mu _{\mathrm {B} }$), découvert en 1911 par le physicien roumain Ștefan Procopiu, est une constante physique nommée en référence au physicien Niels Bohr. Elle relie le moment magnétique de l'électron à son moment cinétique (ou angulaire). C'est une notion similaire au magnéton nucléaire valable pour le proton et le neutron. Le sens physique du magnéton de Bohr est un quantum de moment magnétique pour l'électron, qui correspond au plus petit moment magnétique associé à cette particule.

Le moment magnétique ${\overrightarrow {m}}$ d'une boucle de courant $I$.

Définition

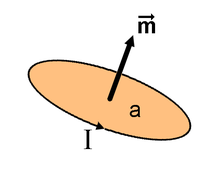
Le magnéton de Bohr est une constante de proportionnalité apparaissant naturellement lors de la quantification des moments cinétiques atomiques. Le moment magnétique ${\overrightarrow {M}}$ est proportionnel au moment cinétique (ou angulaire)${\overrightarrow {L}}$ de l'électron :

${\overrightarrow {M}}=\gamma _{\mathrm {e} }.{\overrightarrow {L}}$

où $\gamma _{\mathrm {e} }$ est le rapport gyromagnétique de l'électron, il vaut :

$\gamma _{\mathrm {e} }=-{\frac {q}{2m_{\mathrm {e} }}}$. (En notant q=e)

Dans le cas de l'atome de Bohr, le moment cinétique ${\overrightarrow {L}}$ est quantifié et vaut :

$||{\overrightarrow {L}}||=n\hbar$

Le moment magnétique de l'électron, peut donc s'écrire :

$||{\overrightarrow {M}}||=n{\frac {q.\hbar }{2m_{\mathrm {e} }}}=n\mu _{\mathrm {B} }$(q = e, on prend la valeur absolue du rapport gyromagnétique car une norme est toujours positive !)

où $\mu _{\mathrm {B} }$ est appelé magnéton de Bohr qui joue le rôle de quantum de moment magnétique pour l'électron.

Valeur

Le magnéton de Bohr $\mu _{\mathrm {B} }$ vaut :

• dans le Système international d'unités :

$\mu _{\mathrm {B} }={\frac {q\cdot \hbar }{2m_{\mathrm {e} }}}$ = 9,274 009 49(80) × 10⁻²⁴ J T⁻¹ (ou A m²) = 5,788 381 755 5(79) × 10⁻⁵ eV T⁻¹

• dans le système CGS :

$\mu _{\mathrm {B} }={\frac {q\cdot \hbar }{2m_{\mathrm {e} }c}}$ = 0,927 × 10⁻²⁰ erg G⁻¹

où

$n$ est le nombre quantique principal,

$q$ est la charge élémentaire,

$\hbar$ est la constante de Planck réduite,

$m_{\mathrm {e} }$ est la masse de l'électron,

$c$ est vitesse de la lumière dans le vide.

Utilisation en physique atomique

Le magnéton de Bohr constitue une unité naturelle pour l'expression du moment magnétique dipolaire de l'électron.

Il est également utilisé pour calculer le moment magnétique des complexes suivant la formule suivante :

$\mu =\mu _{\mathrm {B} }{\sqrt {n_{\mathrm {e} }\;(n_{\mathrm {e} }+2)}}$

avec $n_{\mathrm {e} }$ le nombre d'électrons célibataires appartenant à l'atome central du complexe (sur les orbitales d dégénérées soit eg et t2g)

Voir aussi

Articles connexes

• Constante physique
• Moment magnétique
• Moment magnétique de spin
• Magnéton nucléaire

Bibliographie

• B. Cagnac, L. Tchang-Brillet, J.-C. Pebay-Péroula, Physique Atomique - Tome 1 - Atomes et rayonnement : interactions électromagnétiques, Dunod,  p. 284, 2005 (ISBN 2-10-049228-4).