Graphe complet

Graphe complet
$K_{5}$
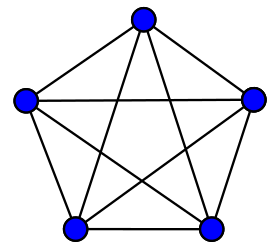Notation	$K_{n}$
Nombre de sommets	$n$
Nombre d'arêtes	$n(n-1)/2$
Distribution des degrés	(n-1)-régulier
Diamètre	1
Maille	∞ si n = 1 ou 2 3 si n > 2
Nombre chromatique	$n$
Propriétés	Hamiltonien, symétrique, régulier

En théorie des graphes, un graphe complet est un graphe simple dont tous les sommets sont adjacents deux à deux, c'est-à-dire que tout couple de sommets disjoints est relié par une arête. Si le graphe est orienté, on dit qu'il est complet si chaque paire de sommets est reliée par exactement deux arcs (un dans chaque sens).

Définitions

Un graphe complet est un graphe dont tous les sommets sont adjacents.

À isomorphisme près, il n'existe qu'un seul graphe complet non orienté d'ordre n, que l'on note $K_{n}$.

Dans un graphe G quelconque, on appelle clique un sous-ensemble de sommets induisant un sous-graphe complet de G. Rechercher une clique de taille maximum dans un graphe est un problème classique en théorie des graphes. Il est NP-complet.

La notion de graphe biparti complet existe également. Mais un graphe biparti complet n'est pas un graphe complet.

Propriétés

Le nombre d'arêtes de $K_{n}$ est :

$\sum _{i=1}^{n}\left(n-i\right)=\sum _{i=1}^{n-1}i={\frac {n(n-1)}{2}}$.

Le premier terme s'obtient en remarquant que la suppression d'un premier sommet de $K_{n}$ entraîne la suppression de $n-1$ arêtes, la suppression d'un deuxième sommet, la suppression de $n-2$ arêtes, et celle d'un i-ème sommet $n-i$ arêtes. Le deuxième terme s'obtient par la même opération en marquant les arêtes au lieu de les supprimer, chaque arête est alors marquée deux fois et l'on fait $n-1$ marquages par sommet (c'est la formule générale de la demi-somme des degrés).

On peut également obtenir cette formule en voyant le nombre d’arêtes comme le nombre de couples distincts que l’on peut former avec $n$ nœuds, soit ${\binom {n}{2}}$ arêtes, ce qui vaut bien ${\dfrac {n(n-1)}{2}}$.

Le graphe complet $K_{n}$ est symétrique : il est sommet-transitif, arête-transitif et arc-transitif. Cela signifie que son groupe d'automorphismes agit transitivement sur l'ensemble de ses sommets, de ses arêtes et de ses arcs. Ce groupe d'automorphismes est de cardinal n! et est isomorphe au groupe symétrique $S_{n}$.

Le polynôme caractéristique du graphe complet $K_{n}$ est : $(x-n+1)(x+1)^{n-1}$. Ce polynôme caractéristique n'admet que des racines entières. Le graphe complet est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers.

Le graphe $K_{5}$ est le plus petit graphe non planaire. Il sert dans les caractérisations des graphes planaires de Kazimierz Kuratowski et de Klaus Wagner.

Conjectures

Nombre de croisements

On note $\mathrm {cr} (G)$ le nombre de croisements du graphe $G$, le nombre minimal de croisements parmi les tracés possibles de $G$. A. Hill et J. Ernest ont conjecturé une valeur pour le nombre de croisements du graphe complet $K_{n}$, que Richard K. Guy a publiée en 1960. On sait qu'il existe toujours un tracé avec

${\textrm {cr}}(K_{n})\leq {\frac {1}{4}}\left\lfloor {\frac {n}{2}}\right\rfloor \left\lfloor {\frac {n-1}{2}}\right\rfloor \left\lfloor {\frac {n-2}{2}}\right\rfloor \left\lfloor {\frac {n-3}{2}}\right\rfloor$

croisements (suite A000241 de l'OEIS). Il est conjecturé que l'inégalité est en fait une égalité. Une formulation indépendante de la même conjecture a été faite par Thomas L. Saaty en 1964.

Saaty a en outre vérifié que cette formule donne le nombre optimal de croisements pour n ≤ 10 et Pan et Richter ont montré qu'elle était également optimale pour n = 11, 12.

Galerie

Pour chacun des graphes complets de 1 à 12 sommets, est indiqué le nombre de ses arêtes.

• 
  $K_{1}$ : 0 arête
  graphe singleton
• 
  $K_{2}$ : 1 arête
• 
  $K_{3}$ : 3 arêtes
  graphe triangle
• 
  $K_{4}$ : 6 arêtes
  graphe tétraédrique
• 
  $K_{5}$ : 10 arêtes
  pentacle
• 
  $K_{6}$ : 15 arêtes
• 
  $K_{7}$ : 21 arêtes
• 
  $K_{8}$ : 28 arêtes
• 
  $K_{9}$ : 36 arêtes
• 
  $K_{10}$ : 45 arêtes
• 
  $K_{11}$ : 55 arêtes
• 
  $K_{12}$ : 66 arêtes