Angle plan
| Unités SI | radian |
|---|---|
| Autres unités | degré, grade, mil angulaire |
| Dimension | 1 |
| Base SI | rad (n'est plus une USI de base). |
| Nature | Grandeur vectorielle extensive |
| Symbole usuel | rad |
| Lien à d'autres grandeurs | |
| Conjuguée | Couple |
| Grandeur duale | Moment cinétique |
L'angle plan est l'angle classique à deux dimensions. On emploie généralement cette expression par opposition à angle solide, l'analogue de l'angle plan dans l'espace.
Il se mesure en radians dans le Système international (SI), alors que l'angle solide se mesure en stéradians. On ajoute généralement ces deux grandeurs aux sept unités fondamentales du SI.
Définition géométrique modifier
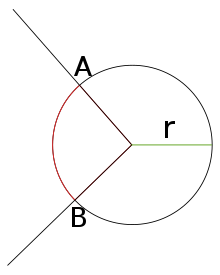
Par définition, en géométrie plane, l'angle plan est la portion du plan comprise entre deux demi-droites, mesurée par la longueur de l'arc (AB) découpé sur un cercle de rayon r centré sur le point d'intersection des deux demi-droites.
La mesure de l'angle en radians est le rapport entre l'arc AB et le rayon r. Étant le rapport de deux longueurs, la mesure d'un angle est donc sans dimension.
En trois dimensions, l'angle séparant deux directions est implicitement un angle plan, scalaire, mesuré dans le plan contenant ces deux directions et le point d'observation. C'est ainsi que l'on peut mesurer, par exemple au sextant, l'écart angulaire entre deux étoiles.
Il ne doit pas être confondu avec l'angle de rotation d'un solide, qui est une grandeur vectorielle (en réalité un pseudovecteur). Ce dernier est défini à partir du champ vectoriel des déplacements des points du solide par rapport à une position d'origine. On montre que ce champ de vecteur est un torseur, caractérisé par un axe de rotation-translation (axe central du torseur, dont les points se sont déplacés parallèlement à l'axe), le vecteur translation le long de cet axe, et un vecteur de rotation autour de cet axe.
Signification physique modifier
Un écart angulaire est dans le mouvement de rotation l'équivalent d'un déplacement dans le mouvement rectiligne. Dans les deux cas, il s'agit d'une grandeur vectorielle.
Le vecteur représentant la rotation a pour direction l'axe de rotation correspondant. Alors que le vecteur d'un déplacement dans le plan est contenu dans ce plan, la rotation dans le plan est donc décrite par un vecteur perpendiculaire à ce plan.
Équations aux dimensions modifier
Depuis la 20e conférence générale du Bureau international des poids et mesures, le radian et le stéradian ont perdu leur statut singulier d'« unités supplémentaires » et sont désormais considérés comme des unités dérivées, « sans dimension dont les noms et les symboles peuvent être utilisés, mais pas nécessairement, dans les expressions d'autres unités dérivées SI, suivant les besoins »[1]. Leur emploi est donc toujours facultatif en ce qui concerne l'expression des unités du Système international d'unités.
Cependant, cette faculté conduit à considérer comme étant de même dimensions des grandeurs physiques qui sont en réalité de nature différente. Par exemple, le moment d'une force s'exprime comme le produit d'une force par une distance, en newton mètre, et a formellement la même dimension qu'une énergie en kg⋅m2⋅s−2. Ce sont cependant deux grandeurs très différentes, l'énergie étant une grandeur scalaire, et le moment d'une force une grandeur vectorielle (un pseudovecteur). De même, une vitesse de rotation est une grandeur mesurée en radian par seconde, qui a formellement la même dimension qu'une fréquence ; cependant la fréquence est un scalaire tandis que la vitesse de rotation est un pseudoscalaire.
D'une manière générale, l'apparition du radian comme « unité » dans l'écriture en unité de base permet de faire la différence entre une grandeur appartenant au domaine des mouvements en rotation, et marque généralement que la grandeur correspondante est un pseudovecteur ou un pseudoscalaire.