Théorème des cercles inscrits égaux

En géométrie, le théorème des cercles inscrits égaux concerne la construction suivante : on trace une suite de segments (les rayons) joignant un point fixé à une droite donnée (la base) telle que les cercles inscrits dans les triangles formés par deux rayons consécutifs et la base aient même rayon. Dans l'illustration, les cercles bleus définissent l'espacement entre les rayons.

Si les cercles bleus ont même rayon, les cercles verts également.

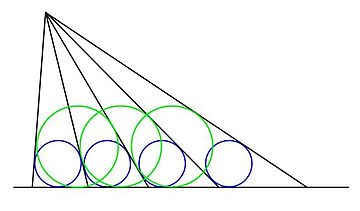
Le théorème stipule que les cercles inscrits dans les triangles formés (à partir d'un segment donné) par un rayon sur deux, un rayon sur trois, etc. et la base ont également même rayon (cf. les cercles verts dans la figure).

Il existe de nombreuses démonstrations de ce théorème. Celles présentées ci-dessous utilisent

• un théorème classique du wasan (mathématiques japonaises traditionnelles) pour la première
• un théorème de Jordan Tabov pour la deuxième
• la trigonométrie hyperbolique pour la troisième

On trouvera dans les références deux démonstrations utilisant un minimum de trigonométrie circulaire, et une autre dans.

Historique

Ce résultat apparaît sans preuve et sans référence en 1991 chez David Wells dans Curious and Interesting Geometry puis dans son édition française, mais vu sa conséquence directe du théorème du wasan ci-dessous, on peut penser qu'il était connu des mathématiciens japonais de la période Edo.

Utilisation d'un théorème du wasan

$h_{1}h_{2}=hh_{3}$

Dans un triangle ABC de cercle inscrit $(3)$ et de hauteur $h$ muni d'une cévienne $[AD]$, on inscrit deux cercles $(1)$ et $(2)$ dans $ABD$ et $ADC$. On note $r_{i}$ le rayon du cercle $(i)$ et on pose $h_{i}=h-2r_{i}$.

Le théorème stipule que $h_{1}h_{2}=hh_{3}$, ce qui peut aussi s'écrire $\left(1-{\frac {2r_{1}}{h}}\right)\left(1-{\frac {2r_{2}}{h}}\right)=\left(1-{\frac {2r_{3}}{h}}\right)$.

Ce théorème peut se démontrer en utilisant les aires, le théorème de Stewart, ou la géométrie hyperbolique.

Il implique directement le théorème des cercles inscrits égaux car si trois cercles bleus consécutifs ont même rayon, il montre que les deux premiers cercles verts ont même rayon, et ainsi de suite.

Utilisation du théorème des quatre cercles de Jordan Tabov

Dans le triangle ABC, on trace cette fois deux céviennes $[AD]$ et $[AE]$, et on considère les cercles inscrits $(1)$ et $(2)$ dans $ABD$ et $AEC$, et les cercles inscrits $(3)$ et $(4)$ dans $ABE$ et $ADC$. Le théorème stipule que $(1)$ et $(2)$ ont même rayon si et seulement si $(3)$ et $(4)$ ont même rayon.

Ce théorème a été prouvé par le mathématicien bulgare Jordan Tabov en 1989, mais il constitue une conséquence et une généralisation d'un théorème publié en 1986 par le Turc Hüseyin Demir.

On en déduit le théorème des cercles inscrits égaux car il montre que les cercles bleus numéros 1 et 3 étant "égaux", les cercles verts numéros 1 et 2 sont égaux, et ainsi de suite. Il montre aussi la réciproque, à savoir que si les cercles verts sont "égaux", les cercles bleus également.

Utilisation de la trigonométrie hyperbolique

Le théorème est un corollaire direct du lemme suivant :

Supposons que le n-ième rayon fasse un angle $\gamma _{n}$ avec la normale à la base. Si $\gamma _{n}$ est paramétré selon la relation $\tan \gamma _{n}=\sinh \theta _{n}$, alors les valeurs de $\theta _{n}=a+nb$, où $a$ et $b$ sont des constantes réelles, définissent une suite de rayons satisfaisant la condition d'isométrie des cercles inscrits, et de plus, toute suite de rayons satisfaisant la condition peut être produite par un choix approprié des constantes $a$ et $b$.

Démonstration du lemme

Dans le schéma, les segments $[PS]$ et $[PT]$ sont des rayons adjacents faisant des angles $\gamma _{n}$ et $\gamma _{n+1}$ avec la droite $(PR)$ perpendiculaire à la base $(RST)$.

La droite $(QXOY)$ est parallèle à la base et passe par $O$, centre du cercle inscrit dans le triangle $PST$, les points de contact étant $W$ et $Z$. De plus, le segment $[PQ]$ a pour longueur $h-r$, et le segment $[QR]$ a une longueur $r$, rayon du cercle inscrit.

Le triangle $OWX$ est semblable à $PQX$, et $OZY$ est semblable à $PQY$ ; de $XY=XO+OY$ on déduit :

$(h-r)(\tan \gamma _{n+1}-\tan \gamma _{n})=r(\sec \gamma _{n}+\sec \gamma _{n+1}).$

Cette relation exprime la condition d'égalité des rayons des cercles inscrits.

Pour prouver le lemme, on pose $\tan \gamma _{n}=\sinh(a+nb)$, qui donne $\sec \gamma _{n}=\cosh(a+nb)$ .

En utilisant $a+(n+1)b=(a+nb)+b$, on applique les formules d'addition pour $\sinh$ et $\cosh$, et on vérifie que la relation d'égalité des rayons des cercles est satisfaite en définissant

${\frac {r}{h-r}}=\tanh {\frac {b}{2}}.$

Cela donne une expression pour le paramètre $b$ en termes de mesures géométriques, $h$ et $r$. Avec cette définition de $b$ on obtient alors une expression des rayons, $r_{N}$ des cercles inscrits formés en prenant chaque N-ième segment comme côtés des triangles

${\frac {r_{N}}{h-r_{N}}}=\tanh {\frac {Nb}{2}}.$

Articles connexes

• Fonction hyperbolique
• Théorème japonais pour les polygones inscriptibles
• Théorème japonais pour les quadrilatères inscriptibles
• Tangentes à un cercle

Liens externes

• Equal Incircles Theorem dans cut-the-knot
• Le théorème des cercles inscrits égaux, par Jean-Louis Ayme, avec historique et bibliographie