Phénomène de Runge

Dans le domaine mathématique de l'analyse numérique, le phénomène de Runge se manifeste dans le contexte de l'interpolation polynomiale, en particulier l'interpolation de Lagrange. Avec certaines fonctions (même analytiques), l'augmentation du nombre n de points d'interpolation ne constitue pas nécessairement une bonne stratégie d'approximation.

La courbe rouge est la fonction de Runge ; la courbe bleue est le polynôme interpolateur de degré 5 et la courbe verte est le polynôme interpolateur de degré 9. L'approximation est de plus en plus mauvaise.

En étudiant cette question, le mathématicien allemand Carl Runge découvrit, en 1901, un résultat contraire à l'intuition : il existe des configurations où l'écart maximal entre la fonction et son interpolation augmente indéfiniment avec n.

Exemple où le phénomène de Runge se produit modifier

Considérons la fonction suivante :

f(x)={\frac {1}{1+25x^{2}}}.

On considère $(n + 1)$ points équi-répartis dans le segment $[-1, 1]$ :

x_{0}=-1,\;x_{1}=x_{0}+h,\;\cdots ,\;x_{k+1}=x_{k}+h=x_{0}+(k+1)h,\;\cdots ,\;x_{n}=1\ {\text{avec}}\ h={\frac {2}{n}}.

Enfin, on considère le polynôme interpolateur de $f$ aux points $(x i)$ , c'est-à-dire l'unique polynôme $P$ de degré inférieur ou égal à $n$ tel que $P (x i) = f (x i)$ pour tout $i$ . On note $P n$ ce polynôme.

Runge a montré que l'erreur d'interpolation entre $P n$ et $f$ tend vers l'infini lorsque n augmente. Autrement dit, plus on fixe de points où le polynôme a la même valeur que $f$ , moins bien on approche la fonction. Formellement :

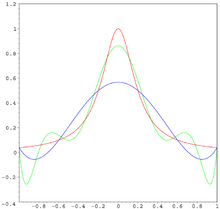
\lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=\infty .

En fait, lorsqu'on augmente le nombre de points, on constate que le polynôme se met à osciller fortement entre les points $x i$ avec une amplitude de plus en plus grande, comme l'illustre la figure.

Explication modifier

Le phénomène de Runge est la conséquence de deux propriétés du problème.

L'amplitude des dérivées de la fonction de Runge augmente très rapidement lorsque n augmente.
L'équi-répartition des points d'interpolation mène à une constante de Lebesgue qui augmente très rapidement lorsque n augmente.

Par applications répétées du théorème de Rolle, on peut montrer que pour le cas d'une interpolation avec n + 1 points équi-répartis, il existe un point $\xi \in ]-1,1[$ tel que

f(x)-P_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0}^{n}(x-x_{i}).

Dans l'exemple choisi, les valeurs des dérivées successives de la fonction augmentent avec le nombre de points, ainsi les oscillations entre chaque point d'interpolation s'amplifient.

De plus, lorsque les nœuds d'interpolation sont équi-répartis, cela empire cette situation, comme cela est expliqué par la suite. En effet, dans un cadre plus général, l'interpolation lagrangienne sur des nœuds équidistants n'est pas la meilleure. En notant ( $l i$ ) la base des polynômes de Lagrange liée aux points ( $x i$ ), on a :

P_{n}(x)=\sum _{i=0}^{n}f(x_{i})l_{i}(x),

dont on tire l'estimation suivante :

\left|P_{n}(x)\right|\leqslant \left(\sum _{i=0}^{n}\left|l_{i}(x)\right|\right)\|f\|_{\infty }\leqslant \sup _{x\in [a,b]}\left(\sum _{i=0}^{n}\left|l_{i}(x)\right|\right)\|f\|_{\infty }.

La constante $\Lambda _{n}=\sup _{x\in [a,b]}\left(\sum _{i=0}^{n}\left|l_{i}(x)\right|\right)$ est appelée constante de Lebesgue associée aux points ( $x i$ ). On remarque que la constante de Lebesgue ne dépend que des nœuds d'interpolation (elle est indépendante de la fonction à interpoler). Dans le cas des points équidistants, cette constante peut être estimée par :

\Lambda _{n}\sim {\frac {2^{n+1}}{{\rm {e}}\,n\ln(n)}},

avec $e$ , nombre d'Euler ou constante de Néper, valant 2,71828… On voit ainsi que dans ce cas, la constante de Lebesgue tend vite vers de grandes valeurs^[1].

Solutions au problème posé par le phénomène de Runge modifier

Le phénomène de Runge met en lumière le fait que l'interpolation polynomiale n'est pas toujours bien adaptée à l'approximation de fonctions.

Choix des points d'abscisse modifier

On peut minimiser l'oscillation des polynômes interpolateurs en utilisant les abscisses de Tchebychev au lieu de points équirépartis pour interpoler. Dans ce cas, on peut montrer que l'erreur d'interpolation (c'est-à-dire $\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|$ ) décroît lorsque n augmente (on peut le voir en étudiant la constante de Lebesgue des points de Tchebychev, à la croissance logarithmique).

Segmentation modifier

Pour approcher une fonction avec des polynômes, on peut préférer utiliser des splines par exemple (ce sont des polynômes par morceaux). Dans ce cas, pour améliorer l'approximation, on augmente le nombre de morceaux et non le degré des polynômes.

Minimisation sous contraintes modifier

Il est possible d'obtenir de bons résultats en cherchant un polynôme de degré supérieur (par exemple 2n), mais en formulant le problème en termes d'optimisation sous contrainte (afin de résorber les degrés de liberté excédentaires). Parmi tous les polynômes croisant la fonction aux points d'interpolation, on recherche celui qui minimise

l'intégrale du carré de sa dérivée première (pénalisation des « pentes raides »).
l'intégrale du carré de sa dérivée seconde (pénalisation des faibles rayons de courbure, polynôme « tendu »).
une combinaison des deux termes précédents.

Il s'agit de minimiser une forme quadratique sous contraintes linéaires, ce qui revient finalement à résoudre un système d'équations linéaires^[2].

Références modifier

↑ Jean-Pierre Demailly, Analyse numérique et équations différentielles, EDP Sciences, coll. « Grenoble Sciences », 2006, 344 p. (ISBN 978-2-7598-0112-1, lire en ligne), p. ?^{[réf. incomplète]}.
↑ Abgrall Rémi, Mathématiques appliquées L3 : cours complet avec 500 tests et exercices corrigés, Pearson, 2009 (ISBN 978-2-7440-7352-6), « Ch. 2, section 2 ».

Annexes modifier

Bibliographie modifier

Jean Dieudonné, Calcul infinitésimal [détail des éditions], chap. IX, appendice, p. 319-320

Voir aussi modifier

On pourra comparer le phénomène de Runge au phénomène de Gibbs qui se produit lorsqu'on interpole des fonctions par des polynômes trigonométriques.

Portail de l'analyse

[1] Jean-Pierre Demailly, Analyse numérique et équations différentielles, EDP Sciences, coll. « Grenoble Sciences », 2006, 344 p. (ISBN 978-2-7598-0112-1, lire en ligne), p. ?^{[réf. incomplète]}.

[2] Abgrall Rémi, Mathématiques appliquées L3 : cours complet avec 500 tests et exercices corrigés, Pearson, 2009 (ISBN 978-2-7440-7352-6), « Ch. 2, section 2 ».

[1]

[2]