Taille apparente

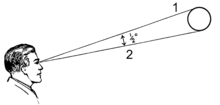
La taille apparente, ou taille angulaire ou diamètre apparent ou diamètre angulaire d'un objet vu à distance est la distance angulaire entre ses points extrêmes au point d'observation, c'est-à-dire l'angle entre les droites qui relient les extrémités de l'objet et l'observateur. On peut relier cette notion à celle d'angle solide ou angle tridimensionnel.

Diamètre apparent d'un astre observé à l'œil nu.

Le diamètre angulaire est la seule mesure directement accessible en astronomie. En topographie ou en navigation maritime, la taille apparente d'objets dont on connaît la dimension permet d'en calculer la distance. Ce calcul suppose que la lumière se propage en ligne droite. Ce n'est pas toujours le cas en astronomie, notamment à proximité d'un corps massif comme une étoile ou à plus forte raison un trou noir.

La taille apparente des objets, lorsqu'elle est estimée sans recours à des instruments, est l'objet d'illusions visuelles qui faussent gravement le jugement. Elle influence la perception des couleurs.

Calcul

Demi-diamètre apparent θ d'un astre.

Le calcul diffère légèrement pour un objet étendu et pour une sphère. Dans les deux cas, on aboutit à une relation approximative linéaire entre distance, taille et diamètre apparent.

Cette notion est utile dans la compréhension des éclipses, avec comme subtilité, la distinction entre une éclipse totale et une éclipse annulaire. On l'utilise aussi en optique géométrique, notamment dans l'étude des télescopes.

Plusieurs méthodes peuvent être utilisées afin de déterminer ou prévoir cet angle.

Cas d'un objet étendu

La taille angulaire d'un objet (δ) en fonction de son diamètre (d) et de sa distance (D).

Un objet ayant une dimension d dans une orientation perpendiculaire à la direction de l'observation, vu centré à une distance D, intercepte un angle δ. La moitié de la dimension de l'objet et les droites qui joignent la position de l'observateur au milieu de l'objet et à une de ses extrémités forment un triangle rectangle, dont l'angle au point d'observation est la moitié de δ, et pour lequel, par définition,

$\tan {\frac {\delta }{2}}={\frac {\frac {d}{2}}{D}}$.

On en tire immédiatement

$\delta =2\arctan \left({\frac {d}{2D}}\right)$.

Pour des objets suffisamment distants, c’est-à-dire tels que la distance D est grande devant la taille d, cette expression peut s'écrire

$\delta \approx {\frac {d}{D}}$ (δ en radians).

Dès D > 3 × d, l'évaluation simplifiée (appelée approximation de Gauss) est correcte à mieux que 1 % près.

On peut donc calculer la distance d'un objet connaissant une de ses dimensions, en mesurant l'angle, en radians ou en milliradians (Mil angulaire). Il faut que la dimension de l'objet dont on estime la distance soit perpendiculaire et centrée sur l'axe d'observation.

Cas d'une sphère

Diamètre angulaire d'une sphère.

Quand l'objet est une sphère, cette condition est remplie quelle que soit la position de l'observateur. La formule exacte diffère de celle d'un objet étendu, la distance étant sur l'hypoténuse du triangle :

$\sin {\frac {\delta }{2}}={\frac {\frac {d}{2}}{D}}$,

d'où :

$\delta =2\arcsin \left({\frac {d}{2D}}\right)$.

L'approximation reste :

$\delta \approx {\frac {d}{D}}$.

Applications terrestres

Mire en topographie.

Le diamètre angulaire peut être utilisé pour calculer la distance à laquelle se trouve l’objet si sa taille réelle est connue.

En topographie, on peut mesurer la distance horizontale en plaçant une toise dont un niveau à bulle indique la verticalité, à un point et en mesurant, à l'autre point, sa taille apparente. Pour éviter le cumul des erreurs, on évite les approximations. La longueur de la toise étant toujours identique, une table donne la correspondance entre l'angle et la distance.

Un télémètre stadimétrique utilisé avec une mire permet de mesurer la distance en mesurant la longueur qu'intercepte un angle fixe.

Amer.

En navigation maritime, une lunette ou des jumelles graduées indiquent la taille apparente d'un objet en mils (milliradians), une expression de la taille angulaire telle qu'un objet de 1 unité de taille vu à 1 000 unités de distance intercepte 1 mil. La description des amers en indique la taille. Un amer de t mètres qui intercepte un angle de m mils est à une distance en kilomètres de t ÷ m. Une grande précision n'est pas nécessaire.

La relation qui donne la distance à partir de la taille angulaire à partir de l'angle au point d'observation, donne aussi la distance d'un point à partir de la différence d'angle de visée depuis une base étendue, dans un télémètre.

La même relation sert en optique géométrique, notamment dans l'étude des télescopes. En optique, la grandeur $\scriptstyle {\frac {1}{D}}$ est la dioptrie, d'usage courant dans les calculs. Les calculs en dioptries simplifient la formule de la distance angulaire en remplaçant le dénominateur. On passe ainsi de la distance focale au grossissement optique, qui est, directement, le multiplicateur de la distance angulaire dans une lunette.

Diamètre apparent en astronomie

En astronomie, le diamètre apparent d'un astre est au départ la seule donnée dont on dispose. Sa distance et sa dimension s'obtiennent par calcul.

Deux objets de taille très différente peuvent avoir la même taille angulaire. Celle de la Lune et du Soleil est d'environ un demi degré (9 mils), mais leur diamètre et leur distance à la Terre diffèrent d’un facteur 400 environ, la Lune étant à 400 000 et le Soleil à 150 000 000 kilomètres.

Diamètres apparents (en minutes et secondes d'arc) du Soleil, de la Lune, des planètes et de planètes naines du Système solaire, observés depuis la Terre

Objet	Minimum	Maximum	Moyen en conjonction inférieure	Moyen en opposition	Réf.
Soleil	31′ 27″	32′ 32″
Mercure	0′ 4,5″	0′ 13″	0′ 11″
Vénus	0′ 9,7″	1′ 6″	1′ 0,2″
Mars	0′ 3,5″	0′ 25,1″		0′ 17,9″
Lune				31′ 36″
Jupiter	0′ 29,8″	0′ 50,1″		0′ 46,9″
Saturne	0′ 14,5″	0′ 20,1″		0′ 19,5″
Uranus	0′ 3,3″	0′ 4,1″		0′ 3,9″
Neptune	0′ 2,2″	0′ 2,4″		0′ 2,3″
Pluton	0′ 0,06″	0′ 0,11″		0′ 0,08″

Cosmologie

En cosmologie, quand la distance devient de l’ordre de la taille de l’Univers observable, il devient nécessaire de prendre en compte l’influence de l’expansion de l'Univers sur le diamètre angulaire des objets. En particulier, pour une taille physique donnée, le diamètre angulaire d’un objet ne décroît pas avec la distance pour des objets suffisamment lointains^{[réf. souhaitée]}.

Cas d'un trou noir

La taille apparente θ d’un trou noir est plus grande que celle d'un objet classique de même rayon. Les effets de déflexion de la lumière que décrit la théorie de la relativité générale le laissent « paraître » plus gros que sa taille réelle. Le trou noir dévie les rayons lumineux passant suffisamment près au point de les absorber. Les calculs montrent qu'un trou noir sous-tend une taille angulaire de :

$\theta ={\frac {3{\sqrt {3}}R_{\rm {S}}}{D}}$, où $R_{\rm {S}}=2{\frac {GM}{c^{2}}}$

R_s est le rayon de Schwarzschild du trou noir, qui peut être considéré ici comme délimitant la « surface » du trou noir (même si en réalité, le trou noir n'a pas de surface matérielle). La formule donne un diamètre angulaire environ 2,5 fois plus grand que ce que l’estimation habituelle donne.

Exemple :

Le trou noir supermassif associé à Sagittarius A*, au centre de notre galaxie, se trouve à une distance de 8,5 kiloparsecs environ. Sa masse, de l'ordre de 2,6 millions de masses solaires, lui confère un rayon de Schwardzschild d'environ sept millions et demi de kilomètres. À une distance de 8,5 kpc, soit 2,6 × 10²⁰ m, son diamètre apparent devrait naïvement être 5,9 × 10⁻¹¹ radian, soit douze microsecondes d'arc. En rajoutant le facteur $\textstyle {\frac {3{\sqrt {3}}}{2}}$ manquant, le diamètre angulaire passe alors à environ trente microsecondes d'arc, qui est désormais accessible à l'interférométrie à très longue base dans le domaine radio.

Perception humaine

Illusion de taille apparente

La Lune semble plus grosse lorsqu'elle est près de l'horizon. Ptolémée, mesurant la taille apparente de la Lune avec des instruments, note déjà qu'il s'agit d'une illusion. On discute depuis de la cause de cette perception.

Le propos de cet article est le cas où l'usage d'un instrument donne une mesure. Dans de nombreux cas comme celui de la taille apparente de la Lune, mais aussi du soleil proche de l'horizon, la perception de la taille est très différente selon qu'on utilise ou non un appareil. En plus des illusions trouvées dans la nature, certaines sont conçues délibérément dans un but architectural, et des expériences comme celle de la chambre d'Ames les mettent en évidence de façon spectaculaire. Les psychologues de la perception ont noté, à la fin du XIX^e siècle, que les perceptions visuelles de la taille et de la distance sont liées. La loi d'Emmert indique que les objets environnants déterminent la taille et la distance perçues d'une image rétinienne. Ce sujet fait encore l'objet d'investigations.

Couleur

La taille apparente des objets affecte légèrement la perception de leur couleur. La Commission internationale de l'éclairage a compilé les tables colorimétriques pour des tailles angulaires de 2°, correspondant à la taille de la macula, en 1931. On s'est rendu compte que ces tables ne prédisent acceptablement la perception des couleurs que jusqu'à une taille apparente d'environ 4°. De nouvelles mesures ont conduit la CIE à publier en 1964 des tables supplémentaires valables pour un angle de 10°.

Annexes

Bibliographie

• Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Bruxelles, De Boeck, 2013, p. 192-193.
• (en) Subrahmanyan Chandrasekhar, The mathematical theory of black holes, Oxford University Press (1983) (ISBN 0198503709).
• Richard Gregory, L'œil et le cerveau : la psychologie de la vision [« Eye and Brain: The Psychology of Seeing »], De Boeck Université, 2000 (1^re éd. 1966).
  • (en) Richard Gregory, Seeing through illusions, Oxford University Press, 2009.

Articles connexes

• Diamètre
• Angle solide
• Distance angulaire
• Distance de diamètre angulaire
• Dioptrie

Liens externes

• Mémoire de DEA, pour comprendre le lien entre diamètre apparent et les éclipses
• http://phys-chimie.voila.net/seconde/physique/chap1/longueur/diametre_apparent/diametre.htm
• http://www.astrosurf.com/denisjarry/diamappa.htm

Notes et références

• Cet article est partiellement ou en totalité issu de l'article intitulé « Taille angulaire d'un trou noir » (voir la liste des auteurs).

• Cet article est partiellement ou en totalité issu de l'article intitulé « Diamètre angulaire » (voir la liste des auteurs).